Leibniz’s Mathematical Approach to God
We
know that Kurt Gödel (1906–1978) worked intensively with Leibniz
(1646–1716) towards the end of his life. Gödel’s obsession with Leibniz
had reached such a degree that, according to Gödel, when some people had
destroyed some of Leibniz’s writings, and Menger asked Gödel, “Who could have an interest in destroying Leibniz’s writings?”, Gödel would say, “Naturally, those people who do not want men to become more intelligent!”
(Menger, 1994). When his friends advised him to focus on his studies,
rather than studying and reading Leibniz’s works, he would not pay
attention to them. Eventually, the expected happened, and Gödel
continued to follow Leibniz’s footsteps and gave God’s ontological proof
like Leibniz.

In this article, I will refer to Leibniz’s work and interpretations, such as his characteristica Universalis
and the binary number system, to give the reader an idea of the part
of his work, particularly about mathematical philosophy. I will also
explain how Leibniz understood the concepts of proof and analytics.
Finally, I will focus on Leibniz’s role in mathematics within the
framework of theology and metaphysics/philosophy.
Characteristica universalis
The Latin term characteristica universalis, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by Gottfried Leibniz able to express mathematical, scientific, and metaphysical concepts. Leibniz thus hoped to create a language usable within the framework of a universal logical calculation or calculus ratiocinator. (Wikipedia, 2019)
Leibniz
was aware that political or philosophical debates and research did not
follow a mathematical method. According to Leibniz, mathematicians are
also likely to make mistakes like everyone else, but they also have some
tools to discover their mistakes. However, philosophers don’t have the
same tools as mathematicians, so they tend to make more mistakes. While there are Aristocians or Platonists in philosophy, there are no ‘Euclidean’ or ‘Archimedean’ in mathematics [God and Mathematics in Leibniz’s Thought, Mathematics, and the Divine: A Historical Study, pages 485–498].
According to Leibniz, it is necessary to mathematize the thought to end
the quarrels that are dominated by feelings rather than righteousness.
In order to formalize a significant part of thought, the symbols and
rules are required to emerge in mathematics. As Leibniz explains in his Preface to a Universal Characteristic,
characteristica universalis will reveal the alphabet of our thinking,
analyze the basic concepts. Based on those concepts, all things will be
judged in a definite manner [Leibniz, G. W. Philosophical Essays, pages 5–10].
Thus, there will be no need for clashes between philosophers who
advocate two different views; they will sit next to each other and say
“calculemus!” (let’s calculate) and they will be able to calculate the
accuracy of their thoughts!
Leibniz’s
idea of characteristica universalis is a type of computational
formulation. This thought was based on matching basic or irreducible
thoughts with prime numbers. A number characterizes every basic thought:
the characteristic number. Let us cite an example given by Leibniz in
his article on Samples of the Numerical Characteristics [Leibniz, G. W. Philosophical Essays, pages 10–18].
Suppose we are given the pairs of numbers (13, 5) and (8, 7), which
refer to the basic concepts of “animal” and “rational,” respectively, in
response to the proposition “Man is a rational animal.” The number that
characterizes the concept of “man” will be ([13 · 8], [-5 · 7]) = (104,
–35). Since there is an infinite number of prime numbers, a number or a
pair of numbers or a triplet of numbers can be assigned to all basic or
fundamental concepts. Other compound concepts can be obtained as the
product of prime numbers, and an entire language can be mapped.
Binary Number System
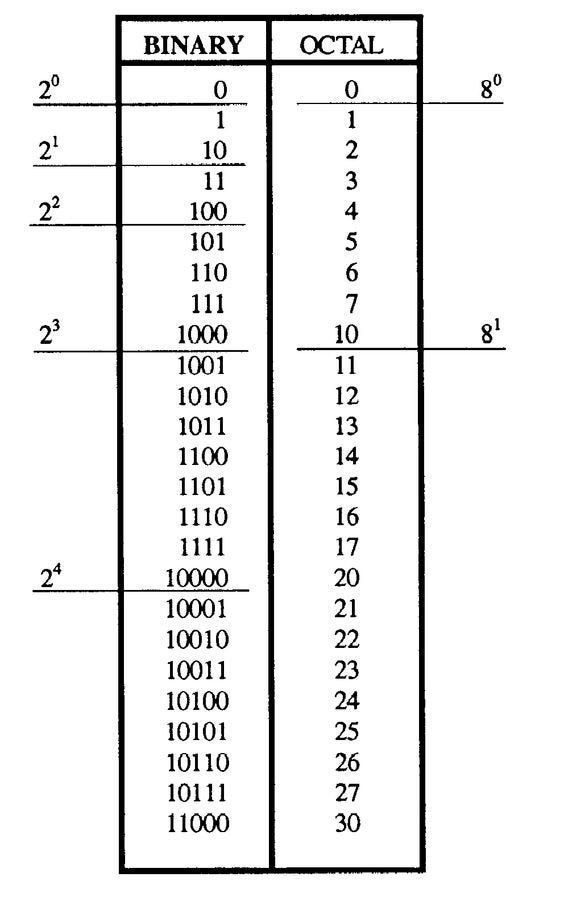
The
binary number system was known before Leibniz, but Leibniz was the
first to record it systematically and maturely. In a letter, Leibniz
wrote about how he dealt with the issue of the creation of everything
out of nothing and the binary number system. That is an example of the
masterful interplay of theology and mathematics (and even physics) in
Leibniz, as I shall mention later.
Leibniz designed a metal medallion (coin) on the creation and the binary system. The medal has the following expressions: Imago creationism (a picture of creation), Omnibus ex nihilo ducendis sufficit unum (In order to produce everything out of nothing one [thing] is sufficient) and Unum est necessarium
(There is need of only one thing). Leibniz, following the Pythagorean
doctrine, claimed that the origin or essence of everything was a number.
As is well known, in the binary number system, all numbers can be
expressed using 0 and 1. Interpreting 0 as “nothingness” and one as
“God,” Leibniz claimed that the binary system symbolized creation so
that everything could be expressed in this system. For Leibniz,
everything is a mixture of 0 and 1. According to this, all things have
come from the One, God.


For
Leibniz, the binary number system revealed the beauty and perfection in
God’s creation. That is, any single number in the binary system may not
appear to be beautiful, but when they are written one under the other,
the beauty appears due to the order within the overall system.
Similarly, there may be things in the world that we don’t like
singularly, but when we get the right perspective, we see that it is
perfect.
Leibniz’s
number mysticism does not end there; he said other things such as “God
loves odd numbers.” Since we do not want to extend this issue, we will
be satisfied with one last example. Leibniz says that the seventh day
after creation is a non-zero (“perfect”) number in the binary system,
adding on to the many numerical analogies that have been made on God’s
creation of the world in six days. It also states that 111 points
represent the Trinity [God and Mathematics in Leibniz’s Thought, Mathematics, and the Divine: A Historical Study].
Modern Proof Concept
As
science philosopher Ian Hacking has shown, Descartes did not know what
proof was in a contemporary sense. Leibniz had a much closer thought to
modern proof (Hacking, 2002). He considered Descartes’ mathematical
accuracy independent of proof. For Descartes, even if an exact thing is
not proved, it is by itself true. Therefore, the truth value of
something and the proof given to it are not related to each other.

Let
us also recall that Descartes is not seeking proof, but rather
practical methods that give new mathematical results. What evokes the
concept of modern proof is that Leibniz realizes a proof is valid, not
due to its content, but because of its form. Accordingly, the proof is a
finite number of sequences of certain sentences according to specific
rules of logic, starting with particular identities. If we recall
Descartes’ method, he attaches great importance to intuition when he is
collecting new information, whereas in a Leibnizian perception of proof,
what is essential is to find “mechanical” proof of the sentence that we
have.
The
ideas of his time probably influenced the idea of proof presented by
Leibniz. As Hacking says (Hacking, 2002 pp. 202), it is customary to
find and remove a person who shook the thoughts deeply before him in
each period; Leibniz plays the role of such a person for his time.
There
is a plausible explanation provided by Leibniz about the emergence of
the idea of proof during his time. It is difficult to reach the
concept of modern proof when the geometry is taken as a measure of
precision: this is because geometric proofs are based mainly on their
“content.” The validity of such proofs is determined by their conformity
with the known properties of the geometric object being studied. With
Descartes’ algebraization of geometry, a way for the proofs to be
transformed into a formal form was opened.
Analytical
The
statements that are a predicate or identical to the subject or the
subject containing the predicate are called analytic. For example, when
we say “all people are alive,” for Leibniz, we mean that the concept of
being alive is within the idea of being human [Leibniz, G. W. Philosophical Essays, page 11], so this statement is analytic. According to Leibniz, all mathematical truths are analytic.
It
is well known that Immanuel Kant (1724–1804) introduced the
analytic-synthetic distinction by diligently transforming Leibniz’s
concept of reality. According to Kant, analytic a priori knowledge is information obtained only by using logic. Synthetic a priori
is the information obtained by using time and space intuition.
According to Kant, arithmetic and geometric lines are synthetic a priori
based on intuition. Here we want to emphasize that Leibniz’s
implications for analytic and righteousness (although Kant has
transformed these meanings) have shaped the basic claims of logicians,
such as Frege and Russell. They attempted to reduce all mathematical
statements to logic in the early 20th century. Moreover, it is likely
that Leibniz’s idea that “axioms can be proved” influenced logicians.
Besides, Leibniz himself tried to present sound proof of the principles
used in a mathematical proof.
Leibniz’s
concept of proof and analytic concept complement each other because the
derivation of any statement from another statement while giving proof
corresponds to the concept of analytics.
Mathematica Divina
So
far, we have touched on some of Leibniz’s views on mathematics. One of
the issues raised in this paper is that Leibniz’s approach to
mathematics cannot be distinguished from his theological and
metaphysical or philosophical views. We have mentioned above that
Leibniz, for example, does not understand the binary number system as an
arithmetical issue. As Breger quoted, for Leibniz, mathematics and
theology were like the steps of a ladder ascending to God” [God and Mathematics in Leibniz’s Thought, Mathematics, and the Divine: A Historical Study, pages 493].
To understand Leibniz, the relationships he assumes between
mathematics, theology, and metaphysics are all matters that need to be
addressed. Such a complex issue cannot be dealt with in detail in this
short article; instead, I will merely address a few points to give the
reader an idea.
Leibniz
hoped that his mathematical achievements would draw attention to his
philosophical and theological ideas; after all, a mathematical
achievement is a sign of a strong mind. This “opportunism” of Leibniz on
a personal level is a reflection of another opportunism on the social
level of his era. As it is known, the Christian missionaries who went to
China used the mathematical achievements of Europe to impress the
Chinese and later Christianize them. Leibniz would approve it without
hesitation. In fact, for Leibniz, the characteristica universalis method
is the safest way to show the truth to those who do not believe in God,
because it will measure and show the accuracy value of everything like a
scales [God and Mathematics in Leibniz’s Thought, Mathematics and the Divine: A Historical Study, page 9].
In other words, the fact that the missionaries show the truth to
non-Christians with this computational method will be enough to lead
them to Christianity!
There is a metaphysical basis for Leibniz to use numbers for characteristica universalis. Leibniz dealt with the belief that “God created everything according to a measure, number, and weight,”
which was also expressed by Plato. Leibniz thinks: some objects have no
weight, so their weight cannot be calculated; some objects do not have
dimensions, so their length cannot be measured, but anything can be
counted. In summary, numbers are the essence of everything. According to Leibniz, God is a perfect mathematician. The act of creation took place with “divine mathematics” (Mathesis quaedam Divina). In his famous essay On the Ultimate Origin of Things, Leibniz says that the origin of all things is a “metaphysical mechanism” or “sacred mathematics” [Leibniz, G. W. Philosophical Essays, page 151].
Everything in the world exists according to certain measures and laws,
and these laws are not only “geometric” but also “metaphysical” [Leibniz, G. W. Philosophical Essays, page 152].
For
Leibniz, a world of free will, even if there exist cruelty and evil, is
better than a world without cruelty, evil and free will, as mentioned
in Theodicy and many other writings. That is the
explanation of God’s creation of a world with evil in it. In all
possible worlds, why did God create this world, not another world, in
this way?
For Leibniz, this is the perfect world! So, as an ideal mathematician, God has calculated all the possible worlds and created the best of them. An example of the best of all possible worlds is that lions are dangerous animals, but without them, this world would be less perfect. Besides, our assessment of the well-being of this world is limited to the events we have known and experienced so far. However, God has chosen this perfect world, taking into account all times and all creations [Leibniz, G. W. Philosophical Essays, page 149–155]. Another example given by Leibniz in this regard is that a person born in prison cannot judge that the whole world is evil by looking around. After all, for Leibniz, individuals see only a particular part, whereas God decides by taking everything into account.
Instead of Results
Leibniz’s
dazzling characteristica universalis program has never happened. David
Hilbert defended a formal mathematical form of Leibniz’s thought and
proposed a program accordingly. Kurt Gödel, who admired Leibniz, proved
the Deficiency Theorem and showed that programs such as characteristica
universalis are doomed to fail, not only in philosophy but even in
mathematics.
Leibniz’s
partly based metaphysics and theology on a mathematical level brought
about serious problems. Leibniz, in a sense, reduced everything to
calculation. For example, he reduced God to a calculator that solved
mathematical questions. It may seem paradoxical, but it is clear that
such a God does not have a say in matters that have no mathematical
solution. Leibniz says that in some places, even God cannot do eternal
operations. When he made God a mathematician, Leibniz understood that
even God was made incapable of where mathematicians were capable. Say,
for example, that God cannot perform infinite operations. Still, he can
see the result (just as the mathematician does not perform infinite
operations one by one while performing limit calculations, but can
calculate the outcome of those infinite operations).
Moreover,
Leibniz did not think that there could be more than one consistent
mathematical system in itself, taking absolute mathematical accuracy.
That raises a problem that Leibniz is not interested in, which
mathematics God uses. Mathematics occupies an important place in all of
Leibniz’s ideas from what we have written so far. According to him, a
mathematician must be a philosopher, just as a philosopher should be a
mathematician. In correspondence with L’Hôpital, Leibniz stated that his metaphysics was mathematical and could be written mathematically [God and Mathematics in Leibniz’s Thought, Mathematics, and the Divine: A Historical Study].
Moreover, according to Leibniz, mathematics is very close to logic; the
art of making new inventions, and metaphysics is no different from
that.
“I started as a philosopher, but as a theologian,”
says Leibniz. Today, if someone wants to understand Leibniz’s
philosophy, they still encounter the main issue; the relationship
between mathematics and philosophy, metaphysics, and theology in
Leibniz’s works.