Cercle π

 

Cercle π-PI (Le nombre mystérieux )

Le cercle on le connaît depuis le temps scolaire, mais qu'y a-t-il d'intéressant là-dedans ? , le monde que vous voyez n'est pas toujours linéaire, une cascade, un lancer de balle, etc. est dans une courbe, pi parle toujours avec une structure semblable à une courbe, il y a 4000 ans, les Égyptiens calculaient l'aire d'un cercle par une formule qui donnait la valeur approximative de 3,1605 pour π.,

Les anciens Babyloniens calculaient l'aire d'un cercle en prenant 3 fois le carré de son rayon, ce qui donnait une valeur de pi = 3. Une tablette babylonienne (vers 1900-1680 av. J.-C.) indique une valeur de 3,125 pour π, qui est un approximation plus proche.

La valeur Pi était cachée dans la nature universelle que nous venons de creuser pour obtenir ces chiffres, Un supercalculateur a calculé Pi à un record de 62,8 billions de chiffres .

Pourquoi PI est là ?

Ce n'est pas grave si cela n'est utile que pour trouver la circonférence, la surface et quelques autres choses, mais cela apparaît dans de nombreux champs non pertinents, quand j'en ai pris connaissance, je n'ai pas pu dormir pendant une nuit.

Aiguille de Buffon

L'aiguille de Buffon est l'un des problèmes les plus anciens dans le domaine des probabilités géométriques . Il s'agit de laisser tomber une aiguille sur une feuille de papier lignée et de déterminer la probabilité que l'aiguille franchisse l'une des lignes de la page. Le résultat remarquable est que la probabilité est directement liée à la valeur de pi.

Stimulation en ligne 
https://mste.illinois.edu/activity/buffon/

Les collisions donnent la valeur pi

La collision de deux boîtes avec deux poids différents , nous obtenons la collision de la valeur pi pourquoi ? personne ne sait, pourquoi pi est là ? ça m'a juste époustouflé

Pour trouver la vitesse orbitale du satellite

v = (2 • pi • R)/T ,équation générale du mouvement circulaire.

où R est le rayon de l'orbite.

Rayon d'orbite

Le rayon de l'orbite peut être calculé à l'aide de l'équation ci-dessus, qui implique également la valeur de pi.

Pour l'équation de champ d'Einstein de la relativité générale :

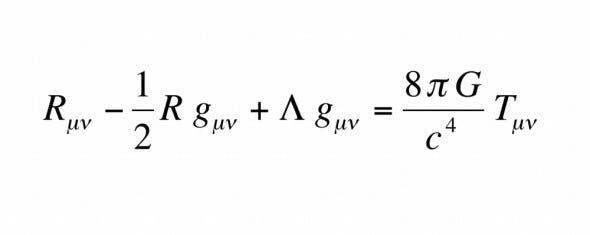
C'est une théorie de la gravité . L'idée de base est qu'au lieu d'être une force invisible qui attire les objets les uns vers les autres, la gravité est une courbure ou une déformation de l'espace. Plus un objet est massif, plus il déforme l'espace qui l'entoure.

Recherche de la valeur de PI

circonférence=2 Π r ,diamètre=2r .

Pour chaque petit à grand cercle de cette terre (je ne suis pas sûr des autres terres du multivers), sa circonférence/diamètre est égal à 3,14…, mais pourquoi 3,141. ? pourquoi pas d'autres numéros ?

Réfléchissons-y…

cette lettre Π sur le côté gauche est nommée d'après la lettre grecque.

PI mot vert signifiant circonférence en anglais, π se prononce comme « pie » (/paɪ/ PY).

la valeur pi ne se termine jamais, comme l'ex GF Lament de mon ami

Allons d'abord faire un cercle…

nous savons Area=𝜋 r², considérons que nous ne connaissons pas la valeur pi pour l'instant, alors comment trouver une aire d'un cercle ?

nous pouvons le couper en morceaux égaux et les fusionner ensemble pour former un rectangle. Nous savons que la formule de l'aire d'un rectangle est l*w.

plus il y a de tranches, plus la valeur de surface que nous pouvons obtenir est précise, donc nous la coupons en n tranches, et la fusionnera avec une erreur minimale.

donc la longueur de ce rectangle est de 1/2 circonférence parce qu'ils ont été réduits de manière égale et fusionnés, puis w est le rayon, pour la circonférence aussi nous avons besoin de pi, nous devons donc obtenir cette valeur qui nous donnera la zone directement pi *r² alors comment trouver la valeur de pi ?

En général, nous savions que tout petit à grand cercle sa circonférence divisée par le diamètre est pi.

nous allons faire un cercle et dessiner un carré au-dessus de ce cercle et à l'intérieur de cet hexagone à 6 côtés. considérant ensuite que l'aire de ce cercle se situe dans ces deux formes.

Ainsi, par la méthode ci-dessus, nous avons appris que pi se situe entre 3 et 4. mais comment en obtenir une valeur assez précise.

Ainsi, en augmentant les côtés de l'hexagone, nous pouvons obtenir une meilleure valeur pi

maintenant en augmentant l'hexagone en 96 côtés, nous obtiendrons

𝜋 >3,1408 et 𝜋 < 3,1429

Le premier calcul de π a été effectué par Archimède de Syracuse (287-212 av. J.-C.). Les 96 côtés ci-dessus sont effectués par Archimède.

Les derniers mots attribués à Archimède sont " Ne dérangez pas mes cercles"   (latin, "Noli turbare circulos meos"; grec Katharevousa, "μὴ μου τοὺς κύκλους τάραττε"), une référence aux cercles du dessin mathématique qu'il était censé étudier lorsqu'il est dérangé par le soldat romain.

Ludolph van Ceulen

Ludolph van Ceulen a passé une grande partie de sa vie à calculer la valeur numérique de la constante mathématique π, en utilisant essentiellement les mêmes méthodes que celles employées par Archimède quelque dix-sept cents ans plus tôt.

Ludolph van Ceulen a découvert 35 chiffres en pi en calculant les milliards et les milliards de côté de l'hexagone

2⁶² = 4 quadrillions de côtés de l'hexagone ===> pour 35 points en pi

Ensuite, après que de nombreux mathématiciens aient essayé plusieurs milliards de côté, mais est-ce vraiment faisable? , le voilà Isaac newton il découvre un meilleur moyen pour cela

nous connaissons la série binomiale

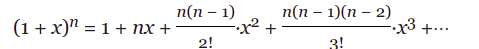
au-dessus ça compte à partir de 0 mais et si ? -1 ou forme m/n qui a été essayée d'Isaac.

si n==-1 
alors 
(1+x)^-1 = 1 − 1x + 1x 2 − 1x 3 + 1x 4 − 1x 5 + ..série continue indéfiniment. 
sinon si n==1/2 
alors 
(1+x)^1/2 = 1+1/2∙x +(1/2)(1-(1/2))x^2/2!+ .. ..série continue pour toujours. si n<1:série continue indéfiniment.

pour l'instant résoudre ci-dessus, nous obtiendrons une série comme

Série de Newton
(1-x²)¹/2= 1–1/2x² +1/8(x)⁴+1/16(x)⁶+….

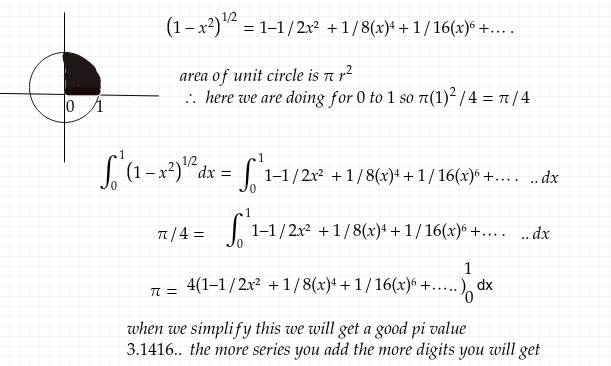
pour la recherche de zone à l'aide de l'intégration, vous pouvez vérifier brillant

Pour obtenir une bien meilleure valeur de pi, newton a essayé l'intégration ci-dessus non pas de 0 à 1 mais de 0 à 1/2, ce qui rendra le terme de calcul plus rapide.

après l'intégration (0,1/2) vous obtiendrez pi =3.14161.., plus vous utiliserez de terme dans la série de newton, plus vous obtiendrez de chiffres

2⁶² =4quadrillions de côtés d'hexagone===> pour 35 points en pi (Ludolph van Ceulen a presque passé 25 ans dans sa vie)

est égal à

calcul du terme série 50 de newton ===> pour 35 points en pi

il y a beaucoup de formules qui sont venues après cet algorithme de Chudonovsky par Ramanujam, Machin - comme des formules…

La valeur Pi est toujours un mystère, ce n'est pas seulement parler avec le cercle, mais toutes les choses géométriques liées à l'espace et au temps et beaucoup d'entre elles, pour nous l'échelle de celle que nous avons dérivée et nous l'avons décidée, mais peut-être que la nature elle-même a une échelle de Pi comme début ou point de départ de quelque chose, il a ouvert de nombreux domaines en mathématiques, en mécanique quantique, etc. et il ouvrira également de nombreux nouveaux...

Les références :

Une brève histoire de Pi (π) | Exploratoire

Une brève histoire de Pi (π) Pi (π) est connu depuis près de 4000 ans, mais même si nous avons calculé le nombre de secondes…

www.exploratorium.edu

Newton et série infinie

Le calcul d'Isaac Newton a en fait commencé en 1665 avec sa découverte de la série binomiale générale (1 + x)n = 1 + nx +…

www.britannica.com

Aire entre les courbes | Wiki Brillant Maths et Sciences

Laisser ...

brillant.org

Approximation de Newton pour pi

Empruntant sans vergogne à Journey Through Genius, nous terminerons l'exemple de la version newtonienne du binôme…

telliott99.blogspot.com

Archimède - Wikipédia

Archimède de Syracuse (; grec ancien : ; grec dorique : [ar.kʰi.mɛː.dɛ̂ːs] ; vers 287 - vers 212 av. J.-C.) était un Grec…

fr.wikipedia.org

Problème d'aiguille de Buffon — Wikipédia

En mathématiques, le problème de l'aiguille de Buffon est une question posée pour la première fois au XVIIIe siècle par Georges-Louis Leclerc, comte…

fr.wikipedia.org

Salmane Faroz

MEDIUM

approche probabiliste

 

Ajouter des nombres infinis : une approche probabiliste de la philosophie mathématique

Illustration de Veronika Vřešťálová

(traduction automatique)

C'est vraiment difficile pour quelqu'un qui aime les mathématiques de s'ennuyer. En effet , les mathématiciens peuvent pje ay des jeux amusants quand ils s'ennuient. Par exemple, ils peuvent jouer à pile ou face avec une pièce qu'ils retirent de leur poche jusqu'à ce qu'ils tombent face et essaient de déterminer combien de temps il leur faut pour jouer au jeu. Ils peuvent même améliorer le jeu et se donner un point pour chaque main jouée. Supposons que vous ayez lancé la pièce et que vous ayez pile. Dans ce cas, vous gagnez un point et lancez la pièce à plusieurs reprises jusqu'à ce que vous obteniez face. Ainsi, pour gagner 10 points, vos neuf premiers lancers doivent être pile et votre dernier lancer doit être face. Ou, pour gagner 3 points, vous devez respectivement obtenir tail-tail-head (TTH). Dorénavant, je parlerai de queues avec T et de têtes avec H.

Probabilité théorique et expérimentale : lancer des pièces

Bien sûr, en passant, nous acceptons que la pièce que nous utilisons est juste, ce qui signifie que la probabilité d'obtenir pile ou face est égale, et 50% comme convenu. Cependant, nous ne pouvons que supposer que la pièce est juste parce que nous ne savons pas si la pièce est juste ou biaisée. On nous dit seulement que la pièce est juste, et nous ne l'avons pas encore prouvé. Alors, comment pouvons-nous être sûrs que la pièce est juste ? En d'autres termes, comment pouvons-nous prouver que la pièce sur laquelle nous parions un flip est juste ?

Tout d'abord, puisque nous sommes des créatures très simples en tant qu'êtres humains, nous ne pouvons jamais comprendre si une pièce est juste ou biaisée en la regardant simplement. Toute pièce peut être légèrement grumeleuse, avec une distribution de poids très non uniforme ; en fait, une pièce en rotation a tendance à tomber plus souvent du côté le plus lourd. Par exemple, retourner un quart américain est assez proche d'être juste, mais il est biaisé vers le côté qui était à l'envers lorsque la pièce a été lancée en l'air. Certains mathématiciens ont prouvé que le rapport est de 51/49 , et non de 50/50 , ce qui est utile à certains prisonniers en Amérique qui connaissent ce fait et utilisent l'information pour gagner de l'argent en jouant au jeu de pile ou face.

Nous pourrions essayer de mettre la pièce à la verticale parce qu'elle ne pourrait pas se tenir debout et basculer si elle est biaisée. Cependant, si la répartition non uniforme du poids est très faible, la pièce peut toujours se tenir debout.

Une scène amusante du film turc, Korkusuz Korkak

Par conséquent, nous pourrions décider que la pièce est juste ou biaisée en la jetant en l'air, mais pouvons-nous conclure à son équité en la lançant en la faisant tourner une ou deux fois ? Si lancer la pièce deux fois ne suffit pas pour parvenir à une conclusion, combien de fois devons-nous lancer la pièce pour décider si elle est juste ou biaisée ? Incidemment, nous ne lançons pas différentes pièces simultanément. Nous lançons une pièce plus d'une fois. Par exemple, si nous prévoyons de marquer la pièce cinq fois, nous la lançons en l'air cinq fois séparément.

Nousne peut pas décider de l'utilité de cet état d'esprit sans essayer de lancer la pièce, c'est pourquoi nous devons le faire plus d'une fois et observer. Notre logique dit que si la pièce est juste, alors obtenir une pile et une face serait suffisant pour déterminer l'équité de la pièce. Si nous lançons une pièce deux fois, nos chances seraient TT, HH, TH, HT, et la probabilité de chaque événement serait de 1/4. Ainsi, la probabilité d'obtenir une pile et une face est de 2/4 ou 1/2. Cela ne prouve toujours pas un point puisque nos chances d'avoir raison sont de 1/2. Par conséquent, si la pièce est juste, mais que nous obtenons deux faces (HH) ou deux faces (TT), on pourrait penser que la pièce est biaisée. Cette déclaration est également valable pour sa position inversée. Par exemple, si la pièce est biaisée et que nous la lançons en l'air deux fois, nous pourrions toujours obtenir une pile et une face, et nous pourrions penser que la pièce est juste.

Malheureusement, la méthode consistant à lancer une pièce deux fois ne fonctionne pas aussi bien.

Essayons de lancer la pièce quatre fois. Ensuite, si la pièce est juste, le nombre d'événements que nous obtiendrons sera de 16 et la probabilité de chaque événement sera de 1/16.

TTTT HHHH TTTH HHHT TTHT HHTH HTTT THHHTTHH HHTT THHT HTTH HHTT TTHH THTH HTHT

Cette fois, pour décider que la pièce est juste après quatre lancers, nous devons obtenir deux faces et deux faces. Il n'y a que six événements lorsque nous obtenons deux têtes et deux queues. Donc, cette fois-ci, la chance que nous ayons raison est de 6/16 ou 3/8 , alors que si nous la retournions deux fois, les chances seraient de 50 %. Comme vous pouvez le voir, plus nous retournons la pièce, moins nous avons de chances de conclure que la pièce est juste. Si nous lançons 1000 fois la pièce, les chances d'obtenir 500 faces et 500 faces seront presque nulles.

Donc, nous ne pouvons pas non plus trouver la réponse à cette méthode.

Si vous êtes physicien, vous pourriez penser que le centre de gravité d'une pièce nous dira si notre pièce est juste ou biaisée. Cependant, ce n'est pas non plus la bonne façon de répondre à notre question car elle s'use chaque fois que nous lançons la pièce et que son centre de gravité change. N'oubliez pas que même un minuscule changement affecte le centre de gravité. D'ailleurs, si le centre de gravité est au milieu de la pièce, comment pouvons-nous trouver le milieu de la pièce pour commencer ?

Il est connu que certaines règles des casinos sont accrochées aux murs pour attirer l'attention, tout comme les articles non modifiables d'une constitution. Avant tout, il est écrit à quel point un dé de casino devrait idéalement être : transparent, symétrique et homogène. Comme le nécessite la structure d'un dé, un de ses côtés est percé une fois, et un autre six fois. C'est pourquoi ils insufflent plus de substance égale à la densité de l'ensemble des dés d'un côté pour maintenir le caractère aléatoire et unique. Deuxièmement, les dés sont constitués de coins nets et pointus pour assurer leur roulement chaotique lorsqu'ils rebondissent sur une table. Si les bords étaient incurvés, les dés se déplaceraient comme un ballon de football et leur probabilité d'atterrir sur un côté serait diminuée. Finalement,les dés devraient être changés presque tous les jours avec de toutes nouvelles versions car même un changement négligeable pourrait avoir un effet significatif sur le caractère aléatoire de son résultat lorsqu'il est lancé.

En résumé, la réflexion théorique ne nous aide pas à tirer notre conclusion ici. Dans la vraie vie, nous ne pourrions jamais comprendre si une pièce ou un dé est juste ou biaisé simplement en le retournant - ce qui signifie qu'une pièce ou un dé juste est un concept purement cognitif. Chaque dé ou pièce est biaisé : le dé ou la pièce juste n'existe pas. Même si nous utilisions des ordinateurs pour produire des dés, ils s'useraient quand nous les lancions et deviendraient biaisés.

Donnons un autre exemple. Disons que vous devez mener une enquête électorale dans un pays avec 50 millions d'électeurs parmi lesquels vous devez choisir 1000 personnes. Lors de la sélection des personnes pour l'enquête, des dizaines de facteurs doivent être pris en compte, tels que le sexe, l'âge, l'emploi, le revenu, la résidence, etc. Les 1 000 personnes sélectionnées peuvent voter uniquement pour le parti A, ou aucune d'entre elles ne peut voter pour le parti. R. Mathématiquement, c'est possible. Cependant, nous n'avons jamais vu ce genre de résultat dans la vraie vie jusqu'à ce jour car la probabilité d'obtenir 0 voix lors d'une élection est extrêmement faible dans un pays de 50 millions d'électeurs.

Par exemple, si 1 000 personnes ont participé à notre sondage et que 450 personnes ont voté pour le parti A, nous nous attendrions à ce que le parti A obtienne 45 % des voix des élections. Cependant, il est presque impossible d'obtenir exactement 45% des voix lors des élections. Le parti A obtiendrait 45.00000000001 des voix, ce qui est différent de 45%. C'est pourquoi il est peu probable qu'il donne un résultat exact en faisant confiance à 1000 personnes sur 50 millions. Alors, comment les sociétés de sondage survivent-elles ? Si j'étais le fondateur d'une société de sondage, je rapporterais plutôt un résultat exact en disant que la partie A obtiendrait entre 0 % et 100 % de participation aux élections.45% des 50 millions de personnes douteront de choisir le parti A car il est impossible d'obtenir les résultats de 1000 personnes sur 50 millions de personnes. Je veux savoir à 100 pour cent s'ils me le demandent. Ensuite, je dirais que le taux que la partie A obtiendrait se situe entre 0 et 100 pour cent. Par conséquent, la société d'enquête estime "entre 40 et 50 pour cent" au lieu de dire "45 pour cent" - grâce à quoi la probabilité de tenir les prévisions électorales augmente.

De même, les sociétés de sondage ne partagent pas les résultats exacts et appliquent un « écart type » à leurs données. Par exemple, ils disent que le parti A obtiendra probablement entre 40 et 50 % des voix. Ensuite, la probabilité de leurs prédictions augmente beaucoup.

Le diagramme d'écart type

En mathématiques, de tels calculs et écarts sont effectués avec un fait mathématique remarquable appelé distribution gaussienne ou distribution normale. J'ai rencontré la distribution gaussienne pour la première fois dans un musée. Il y avait un jouet appelé Galton Board , et il y avait des milliers d'épingles qui suivaient un motif géométrique particulier sur une surface noire. Lorsque vous avez laissé tomber des billes sur la broche supérieure, elles ont rebondi vers le bas. Lorsqu'une bille touchait une épingle, elle rebondissait à gauche ou à droite avec une probabilité égale de 50 %.

Le Galton Board : 3000 billes d'acier tombent à travers 12 niveaux de chemins de branchement et finissent toujours par correspondre à une distribution de courbe en cloche. | Source : Quanta Magazine

De plus, chaque bille a suivi un chemin différent en raison de l'imprévisibilité. Regarder les mouvements aléatoires des billes était très satisfaisant. Mais ce qui rendait le Galton Board unique, c'est que chaque fois que je laissais tomber des milliers de billes, j'obtenais presque la même forme avec un minimum de différences ! Je ne pouvais pas prédire l'emplacement exact d'un marbre, mais je pouvais distinguer la forme exacte que nous obtenions. Cela s'appelait la distribution normale, et c'était "supercalifragilisticexpialidocious". Nous laissions tomber des billes au hasard, les billes rebondissaient au hasard, mais nous obtenions toujours la même forme !

Bien sûr, il y a une loi mathématique derrière l'incident, et elle est étonnamment liée au corps humain. Nous savons que le nez, les oreilles, les yeux et la bouche de chaque être humain ont une place particulière sur leur visage. Oui, certains d'entre nous ont un nez légèrement courbé ; d'autres ont des arcs, mais les emplacements de nos yeux et de nos oreilles sont apparents. S'il n'y avait pas de distribution normale dans la nature, tout le monde ressemblerait aux personnages des œuvres de Picasso , avec nos jambes et nos bras placés à des endroits disparates sur notre corps.

Exemples d'œuvres de Picasso : À gauche : Femme assise dans un fauteuil | A droite : femme assise

Voilà une belle idée de projet que vous pouvez réaliser avec votre enfant ou vos élèves !

Essayez ce beau projet sur Abakcus.com

Quoi qu'il en soit, revenons à notre sujet. Nous avions prévu de lancer une pièce en l'air jusqu'à ce que nous ayons face. Nous voulions aussi jouer à ce jeu autant que nous le pouvions et prédire sa fin.

Bien sûr, le jeu pourrait se terminer si nous obtenions face, ou il pourrait se terminer en 5 ou 32 coups. Le nombre de coups varie d'une personne à l'autre : je pouvais obtenir la tête après dix lancers alors que vous pouviez l'obtenir après trois lancers. Ou si quelqu'un est très malchanceux, il pourrait avoir la tête à son premier lancer. Nous ne pouvons donc pas avoir de nombre moyen de lancers ni d'attentes.

Pour faire des mathématiques, cependant, nous avons besoin d'attentes rationnelles. Là où il n'y a pas d'attentes, il n'y a pas de science.

Par exemple, est-il possible de voir de la neige en plein été ? Oui c'est le cas. Mais les attentes de la plupart des gens seraient le contraire. Si quelqu'un vient vous dire qu'il n'y aura pas de neige le 23 août 2020, vous ne direz pas : « Oh, tu es un génie ! Comment saviez-vous que?"

Laissant tout de côté, il faut penser à la fin de ce jeu : va-t-il finir ou pas ? Mathématiquement parlant, notre jeu peut durer éternellement si la pièce que nous tirons donne toujours pile. C'est possible! C'est pourquoi nous devons déterminer s'il y a une fin à ce jeu ou non ! Disons que notre professeur de mathématiques nous donne des devoirs, dans lesquels nous devons lancer une pièce et toujours obtenir pile. On essaie à la maison : on lance une pièce et on obtient face, et on a tout de suite terminé. Mais peut-être que si nous jouions un autre tour, nous pourrions continuer encore quelques tours avant d'avoir des têtes. Donc, nous redémarrons et retournons à nouveau la pièce, et nous obtenons respectivement TTTTTTTTTTH ; le jeu est toujours terminé. Aucun problème! Nous pouvons réessayer. Nous nous embarquons donc dans un voyage où nous obtenons toujours des queues (juste en supposant). Mais comment jouer éternellement ?La mort est inévitable, et donc tout le monde meurt ! Comme vous pouvez le voir, nous ne pouvons que deviner ou parler en théorie. Dans la vraie vie, obtenir des queues pour toujours est impossible !

Àconclure de tout ce dont nous avons parlé, il est en effet plus logique de calculer le nombre moyen de lancers de pièces qui aboutiraient à des têtes. Premièrement, si nous approchons intuitivement, nous pouvons tirer des conclusions immédiates. Par exemple, le nombre moyen de lancers de pièces pour obtenir face doit être supérieur à 0 car il faut jouer au moins une fois. De plus, si notre jeu se termine par un seul flip, c'est-à-dire si notre premier flip tombe sur face, un facteur de chance sera impliqué. Nous devrons éliminer ce facteur de chance en jouant plusieurs fois au jeu. Enfin, la moyenne ne peut pas être aussi grande que huit, car il est peu probable que l'on obtienne sept queues consécutivement (TTTTTTTH).

Au fait, comment trouve-t-on la moyenne ? Par exemple, si nous obtenons face au troisième lancer, nous gagnerons 3 points. Ensuite, si nous obtenons face au premier lancer, nous gagnerons 1 point. Ensuite, la moyenne sera (3+1)/2 = 2. Nous continuerons à jouer au jeu plusieurs fois comme ça, et nous trouverons la moyenne en collectant les points reçus et en divisant le nombre résultant par le nombre de fois que nous avons joué le jeu.

Maintenant, que diriez-vous de jouer à ce jeu un milliard de fois ? Eh bien, c'est techniquement impossible car une durée de vie moyenne de 80 ans équivaut à 2 milliards de secondes. En pratique, une telle chose n'est pas possible et n'a aucun sens. Ainsi, nous ne savons pas si ce jeu se terminera ou non, mais au moins nous avons appris que nous pouvions jouer à ce jeu un nombre infini de fois dans notre esprit.

La première pièce que nous lancerons se traduira par des têtes ou des queues. Si c'est face, le jeu sera terminé et nous obtiendrons le point. Si c'est pile, nous obtiendrons le point et le jeu continuera. Il n'y aura que deux possibilités : pile ou face. De cette façon, nous allons maintenant jouer au jeu n fois et noter tous les scores que nous avons reçus. Appelons ce total t. Alors notre espérance sera t sur n (t/n) . Mais permettez-moi de le répéter, ce nombre t/n sera purement un concept philosophique car il n'a aucune utilité dans la pratique. Disons que notre attente réelle pour comprendre si une pièce est biaisée est de cinq et que le t/n moyen est de 5,01. Dans ce cas, on ne peut pas dire que la pièce n'est pas biaisée. Nous recherchons la vérité absolue.

Imaginons maintenant que nous ayons joué à ce jeu un milliard de fois, dont la moitié s'est très probablement terminée en un seul coup. Ensuite, nous jouerons 500 millions de fois et collecterons 500 millions de points. Deux cent cinquante millions de parties seront terminées en deux coups, et nous récolterons à nouveau 500 millions de points. Cent vingt-cinq millions de parties seront terminées en trois coups, et nous obtiendrons 125 millions x 3 points. Si nous formulons ;

t/n = (500 millions x 1 + 250 millions x 2 + 125 millions x 3 + ….) / 1 milliard.

Lorsqu'il est simplifié ;

t/n = [1/2¹ x 1] + [1/2² x 2] + [1/2³ x 3] + … (jusqu'à un milliard)

Comme je l'ai mentionné plus haut, nous avons dû éliminer le facteur chance. Maintenant que nous avons joué à ce jeu un milliard de fois, nous avons réduit le facteur chance à presque zéro. Mais nous ne pouvions toujours pas atteindre zéro, pas complètement. Pour éliminer le facteur chance, nous devons prendre le nombre de jeux auxquels nous jouerons (n) jusqu'à l'infini. Donc, l'attente doit être ;

t/n = [1/2¹ x 1] + [1/2² x 2] + [1/2³ x 3] + … à l'infini.

L'équation ci-dessus est une somme infinie. Avez-vous déjà ajouté des nombres infinis dans votre vie ? En fait, nous avons souvent fait des sommes infinies, mais nous n'avons jamais su ce que signifiaient des sommes infinies.

Nous avons tous entendu parler du nombre pi (3,1415926… ). Pi va toujours sans se répéter et est plein de surprises; calculer Pi est aussi passionnant !

Nous pouvons trouver Pi en divisant la circonférence d'un cercle par son diamètre. Cependant, ce n'est pas aussi facile qu'il y paraît. Par exemple, nous ne pouvons jamais obtenir une valeur absolue en ramassant une corde, en l'enroulant autour de la roue de notre vélo et en mesurant la longueur. Ce que nous pouvons faire, c'est trouver une valeur approximative. Par exemple, mesurons la circonférence de la roue du vélo comme 7-quelque chose. Alors qu'est-ce que c'est que quelque chose ? Soit 7,45. Alors quoi ? Nos yeux ne sont pas assez forts pour trouver le nombre suivant. Nous devrons peut-être regarder la corde que nous utilisons pour mesurer la circonférence de la roue avec un microscope.

Picycle

Parce qu'il s'agit d'un travail de terrain, il peut suffire d'accepter le nombre de pi comme 3,14. Cependant, pour faire une superbe montre suisse, il est nécessaire de connaître les 40 à 50 premiers chiffres du Pi. Il faut 46 chiffres de Pi pour aller dans l'espace. Lorsque nous marquons deux points et essayons de mesurer la distance entre eux à l'aide d'un télescope, ils s'avèrent énormes. En un mot, Pi est une construction cognitive : il n'y a pas de cercle parfait. Une ligne peut être unidimensionnelle par définition, mais si nous traçons une ligne au tableau maintenant, elle sera tridimensionnelle. Une ligne va aussi à l'infini, mais nos dessins sont finis. Ainsi, le nombre Pi est purement cognitif.

Lorsque nous écrivons chacun de ces termes l'un après l'autre et que nous les ajoutons, nous obtenons le nombre pi. Si pi est 3.1415926… On peut l'écrire comme :

3 + 1/10 + 4/10² + 1/10³ + 5/10⁴ + …3 
0,1 
0,04 
0,001 
0,0005 
0,00009 
0,000002 
0,0000006 
.......... 
........... 
............ 
+__________________

Lorsque nous collectons des nombres infinis, nous suivons un chemin différent. Nous commençons généralement à ajouter à partir de l'extrême droite, mais comme Pi n'en a pas, nous devons commencer à ajouter à partir de l'extrême gauche. Inventons un autre exemple de somme infinie.

2.357911131719232931374143475361... est un nombre composé de nombres premiers, et il ne se termine jamais.1.2345678910111121314151617181920... est un nombre qui se compose de nombres naturels et s'étend indéfiniment.

Essayons maintenant d'ajouter ces nombres. Typiquement, si ces nombres sont finis, l'addition est facile, mais malheureusement, ces nombres sont infinis. Nous devons calculer différemment.

2.357911131719232931374143475361.... 
1.2345678910111121314151617181920... 
+__________________________________________

La partie entière semble être 3, mais nous ne pouvons pas en être sûrs. Ce total est certainement supérieur à 3. De plus, comme le premier nombre est inférieur à trois et le deuxième nombre est inférieur à 2, leur somme est certainement inférieure à 5. Le total est donc censé être 3-quelque chose ou 4-quelque chose.

En d'autres termes, la somme est supérieure à trois mais inférieure à 5.

Si nous allons un peu plus loin, le premier nombre est supérieur à 2,3 , l'autre est supérieur à 1,2, donc le total est supérieur à 3,5. Le premier nombre est inférieur à 2,4 et le deuxième nombre est inférieur à 1,3. Le total est donc inférieur à 3,7. Nous devrions être un peu plus près de la réponse absolue.

Ainsi, la somme est supérieure à 3,5 mais inférieure à 3,7.

Nous allons passer un chiffre de plus pour nous rapprocher un peu plus de cela. Le premier nombre est supérieur à 2,35 et le deuxième nombre est supérieur à 1,23, donc le total est supérieur à 3,58. De plus, le premier nombre est inférieur à 2,36 et le deuxième nombre est inférieur à 1,24, le total est donc inférieur à 3,60.

Or, la somme est supérieure à 3,58 mais inférieure à 3,60.

En généralisant à partir de cet exemple, où nous avons essayé d'ajouter deux nombres infinis, a et b, nous ne savions pas comment trouver a + b. Nous avons donc d'abord résumé les nombres fractionnaires inférieurs à a et b et avons trouvé une limite inférieure. Ensuite, nous avons ajouté les nombres fractionnaires supérieurs à a et b et avons trouvé une limite supérieure. Nous avons réalisé que la somme de a + b est quelque part entre la borne inférieure et la limite supérieure. S'il y a un écart entre la borne inférieure et la borne supérieure, nous ne pourrons pas connaître la valeur exacte de a + b. Par conséquent, nous parlons de l'existence d'un nombre dans une plage après avoir rapproché les limites inférieure et supérieure l'une de l'autre.

La logique fonctionne exactement comme démontré ici. Comme on l'a vu, nous ne savions pas quel était le total exact. Nous pensions seulement connaître le total réel et nous avons répété de simples ajouts.

Revenons à l'équation ci-dessus. Maintenant;

Maintenant, nous voulons déterminer la somme infinie det/n = [1/2¹ x 1] + [1/2² x 2] + [1/2³ x 3] + … à l'infini.

Cependant, nous ne savons pas ce que cela signifie d'ajouter des nombres infinis. Dans l'exemple précédent, nous ajoutions deux nombres. Nous allons maintenant essayer d'ajouter un nombre infini.

- Au premier lancer, c'est face et nous avons obtenu 1 point avec 1/2 probabilité. 
- Au deuxième lancer, TH est venu, et nous avons obtenu 2 points avec 1/4 de probabilité. 
- Au troisième lancer, TTH est venu, et nous avons obtenu 3 points avec 1/2³ de probabilité. 
- .........Comme vous pouvez le voir, ce processus peut durer éternellement.

Disons que la somme des points que nous avons obtenue est b. De plus, puisque nous jouerons à ce jeu un nombre infini de fois, les queues viendront à chaque fois que nous lancerons, donc; TTTTTTTTT… Est-ce probable ? Puisque toutes les probabilités seront 1, nous pouvons écrire une équation comme celle-ci :

(1/2 + 1/4 + 1/8 + 1/16 + ……) + p = 1La partie gauche avec parenthèses est la probabilité de terminer le jeu, p est la probabilité de ne pas terminer le jeu. Si nous pouvons trouver la valeur de p, nous trouverons nos attentes.

Si vous regardez les nombres fractionnaires entre parenthèses, vous remarquerez une équation fascinante. Essayons d'aller du point A au point B, la distance entre étant de 1 mètre. Notre condition est d'aller à chaque fois à mi-chemin. Faisons donc d'abord la moitié de la route (1/2), puis la moitié du reste (1/4), puis la moitié du reste (1/8), etc. Essayons maintenant d'ajouter les distances que nous avons parcourues.

b= 1/2 x 1 + 1/2² x 2 + 1/2³ x 3 + …

Puis,

1/2 = 0,5 
1/4 = 0,25 
1/8 = 0,125 
1/16 = 0,0625 
1/32 = 0,03125 
1/64 = 0,015625 
1/128 = 0,0078125 
1/256 = 0,00390625 
1/512 = 0,001953125 
1/1024 = 0,0009765625 
1/2048 = 0,00048828125 
....................... 
................................ .. 
.........................

Comment additionner des nombres infinis ? La collection normale commence à l'extrême droite, mais comme nous n'avons pas de chose appelée «extrême droite» dans un nombre infini, nous devons recommencer à l'extrême gauche.

Ne se pourrait-il pas que tous les nombres soient supérieurs à 0 et inférieurs à 1, mais que le total soit supérieur à 1 ? Cela ne peut pas parce que cette somme infinie plus le nombre p doit être égal à 1. Si la somme des nombres les plus à gauche est en quelque sorte 1, alors le total sera sans aucun doute supérieur à 1, mais il doit être 1. Donc ce total sera 0-quelque chose .

Ajoutons les premiers chiffres après la virgule. 5 + 2 + 1 = 8. Le total est donc supérieur à 0,8. Mais après un certain temps, ce nombre sera de 0,9. Comment savons-nous cela? Lorsque vous ajoutez les deuxièmes chiffres suivants à votre point, 17 arrive, il y aura donc un total de 8 à la fois. Lorsque nous ajoutons les chiffres suivants, nous verrons que la somme de tous les chiffres sera 9.

Le total sera de 0.99999999…. Les neuf dureront éternellement.

Nous allons maintenant soustraire la somme que nous avons trouvée de 1 pour trouver p.

1 – 0,9999999999... = p

Puis,

1 
0,999 
-_______ 
0,001

Et

1 
0,9999 
-_______ 
0,0001

Lorsque nous faisons cette soustraction avec des neuf infinis, il semble que nous mettrons 1 à la fin du résultat. Mais supposons que cette soustraction soit égale au nombre « a » à la place. Si on multiplie a par 10,

a = 0,0000000000………… 1 
10a = 0,0000000000………… 1 à nouveau. Exactement la même chose. Ainsi;10a = a 
9a = 0 
a = 0.

En fait, ce que nous avons fait en dernier est faux. S'il existe un nombre tel que 0,000000…………… 1, nous ne saurions pas comment multiplier ce nombre par 10.

Fait amusant, la grande majorité des gens connaissent le nombre 0.9999999999… comme inférieur à 1, mais ce nombre est en fait égal à 1. L'erreur vient du fait qu'ils ne connaissent pas la somme infinie.

0.9999999999… est juste sous le nez de 1. On ne peut pas dire qu'il est proche de 1 car 0,9999999… est également proche de 2. C'est pourquoi on dit que c'est juste sous le nez de 1.

0,9999999… par définition est égal à 1.Donc, si 0.999999... + p = 1, alors p=0.

Le jeu est terminé. Bien sûr, théoriquement. En pratique, cela n'a aucun sens.

Ali

Professeur de mathématiques. Conservateur de contenu. Joueur de football. Fan de Maradona. Surtout écrire sur les conférences que j'aime mieux apprendre. alikayaspor@gmail.com

29K abonnés

Cet article est écrit à partir d'une des conférences d' Ali Nesin sur Youtube.