théorie quantique des champs

 

La théorie quantique des champs

(traduction automatique)

L'explication la plus simple de la plus belle théorie quantique de la réalité

"J'avais entrepris de réfuter la théorie quantique des champs - et c'est le contraire qui s'est produit ! J'étais choqué."

— David Gross, physicien théoricien et lauréat du prix Nobel

Quand nous étions à l'école, on nous a appris que chaque matière est composée de minuscules petites particules appelées atomes ayant une masse centrale concentrée appelée noyau. Le noyau contient des protons chargés positivement et des neutrons sans charge. Il y a aussi des électrons qui tournent autour du noyau. Si vous êtes un étudiant universitaire, cette même chose est enseignée d'une manière légèrement différente et un peu plus avancée, que les protons et les neutrons ne sont pas des particules élémentaires car ils sont en outre constitués de quarks. Cela signifie que l'univers est composé d'une combinaison d'électrons et de quarks. Mais est-ce complètement vrai ?

Essayons de comprendre cela. L'univers n'est pas seulement composé d'électrons et de quarks, car dans ce modèle, nous ne pouvons pas savoir comment fonctionnent les différentes forces et de quoi sont faits ces quarks, électrons, etc. Nous préférons souvent parler de théorie des cordes, de mécanique quantique et de sujets tels que le multivers parce que nous avons entendu parler de ces termes à un moment donné quelque part et nous trouvons ces sujets très fascinants. Mais il existe aussi une telle théorie que la plupart d'entre nous ne connaissent pas, ou du moins ne comprennent pas. Cette théorie est la théorie quantique des champs.

Photo de Zoltan Tasi sur Unsplash

Afin de comprendre l'univers, la théorie quantique des champs est l'une des meilleures théories car la plupart des prédictions faites par QFT se sont avérées vraies et il fonctionne mieux pour décrire la plupart des phénomènes physiques et le comportement de l'univers à un grand Le degré. Classiquement, QFT est souvent considéré comme un concept compliqué. Dans cet article, je vais essayer d'expliquer les bases de la théorie quantique des champs d'une manière aussi simple et compréhensible que possible.

Avant de commencer à en savoir plus sur QFT, essayons de comprendre ce que le modèle standard de la physique des particulesest. Il fut un temps où les scientifiques croyaient que les atomes étaient les plus petites particules de matière et qu'ils ne pouvaient plus être divisés. Ensuite, nous avons compris que les atomes ne sont pas vraiment les plus petites particules et qu'ils sont constitués de particules subatomiques - protons, neutrons et électrons. Lorsque la théorie quantique est entrée en jeu au milieu des années 1930 et 1940, elle a prédit l'existence de nouvelles particules, avec lesquelles nous n'étions pas familiers jusqu'à présent. Afin de comprendre ces particules nouvellement prédites, nous avions besoin de nouvelles théories. Lorsque ces nouvelles théories ont été formulées, elles ont prédit l'existence de quelques particules plus élémentaires. Plus tard, lorsque nous avons brisé les particules déjà existantes dans les accélérateurs de particules à haute énergie, nous avons découvert de nouvelles particules prédites. Avec les découvertes croissantes de nouvelles et nouvelles particules élémentaires,masse, spin, charge électrique, etc. Cela a donné naissance à un modèle pouvant tenir dans toutes les particules fondamentales réparties selon leurs propriétés intrinsèques. Le modèle a non seulement organisé ces particules, mais a également fourni un moyen d'expliquer les forces fondamentales de la nature en ce qui concerne leurs porteurs de force correspondants. Ce modèle est connu sous le nom de modèle standard de la physique des particules.

Modèle Standard. Image Wikimédia Commons. Source : Laboratoire Fermi

Comprenons ce que sont ces particules dans ce modèle et quels sont leurs rôles dans l'univers. Toutes les particules présentes dans l'univers se répartissent principalement en deux catégories : les bosons et les fermions. Les fermions sont responsables de la construction de la matière, que ce soit une table, un arbre, un livre ou un animal. Alors que les bosons sont les porteurs de force. La famille Fermionic est divisée en Quarks et Leptons. Il existe au total six types de quarks différents : Up, Down, Charm, Strange, Top et Bottom. Ils forment des protons et des neutrons à l'intérieur du noyau d'un atome. Les quarks ne sont pas des particules stables, ils se combinent donc en un groupe pour former des hadrons. Les hadrons sont ensuite divisés en mésons et baryons. Les particules baryoniques (protons et neutrons) sont formées par la combinaison de trois quarks. Les protons sont constitués de deux quarks Up et d'un down alors que les neutrons sont constitués de deux quarks down et d'un up. Les quatre types de quarks restants se combinent pour nous donner d'autres nouvelles particules. Les leptons, d'autre part, sont ces particules qui ne sont pas formées par des quarks, comme le muon, les électrons, le tau, le neutrino , etc. Ce sont des particules stables et, par conséquent, elles n'ont pas à se combiner les unes avec les autres pour former d'autres particules et ils peuvent exister indépendamment.

Le principe d'incertitude de Heisenbergprédit l'existence de ces particules qui existent sans aucune cause, et leur existence est probabiliste. Ces particules sont appelées particules virtuelles. De telles particules virtuelles sont trouvées expérimentalement. Indépendamment de la bizarrerie de ces particules, elles ont toujours tendance à suivre un certain schéma spécifique. Ces particules viennent toujours par paires. Ces paires contiennent deux types de particules dont l'une est une particule de matière régulière et l'autre est une particule d'anti-matière. Les particules d'antimatière sont les particules qui ont la même masse que les particules de matière mais qui ont des charges opposées. Lorsqu'un électron se forme, il se forme également une particule d'antimatière à côté de laquelle on appelle un positon, ou un électron positif. Lorsque ces particules matière-antimatière entrent en collision, elles s'annihilent pour produire de l'énergie pure. Comme les électrons, tous les autres leptons ont aussi leur paire d'antimatière. Les bosons sont de quatre types : les photons, les bosons W/Z, les gluons et les gravitons. Jusqu'au début du 19e siècle, les scientifiques croyaient que l'électricité et le magnétisme étaient deux forces différentes. Nous savons maintenant que ces deux forces ne sont que des formes différentes de la même force appelée force électromagnétique. L'électricité, la lumière visible, etc. sont les résultats de la force électromagnétique. Cette force est portée par les photons. Nous faisons l'expérience de ce type de force chaque jour dans nos vies, l'une ou l'autre forme. La force nucléaire faible est la deuxième force la plus faible de toutes qui est responsable de la désintégration bêta. Les bosons W/Z sont responsables du transport de cette force. La force nucléaire forte est la force la plus puissante de toutes qui est responsable de la liaison des nucléons (protons et neutrons) ensemble dans le noyau d'un atome. Les gluons sont les particules chargées de transporter une force nucléaire forte. La force gravitationnelle est la plus faible de toutes les forces fondamentales qui sont hypothétiquement portées par les gravitons. Malheureusement, nous n'avons pas découvert l'existence de telles particules, mais leur existence a été prédite par de nombreuses théories importantes. Jusqu'à présent, nous avons appris sur les particules de matière et la force transporte dans le modèle standard. Il existe cependant un autre type de particule dans la liste appelée boson de Higgs, qui est principalement responsable de fournir de la masse à l'autre particule. Je partagerai l'histoire du boson de Higgs dans un autre numéro. nous n'avons pas découvert l'existence de telles particules, mais leur existence a été prédite par de nombreuses théories importantes. Jusqu'à présent, nous avons appris sur les particules de matière et la force transporte dans le modèle standard. Il existe cependant un autre type de particule dans la liste appelée boson de Higgs, qui est principalement responsable de fournir de la masse à l'autre particule. Je partagerai l'histoire du boson de Higgs dans un autre numéro. nous n'avons pas découvert l'existence de telles particules, mais leur existence a été prédite par de nombreuses théories importantes. Jusqu'à présent, nous avons appris sur les particules de matière et la force transporte dans le modèle standard. Il existe cependant un autre type de particule dans la liste appelée boson de Higgs, qui est principalement responsable de fournir de la masse à l'autre particule. Je partagerai l'histoire du boson de Higgs dans un autre numéro.

Les champs quantiques créent des forces fondamentales. Source : Youtube

Les particules porteuses de force, les bosons, ont été prédites par la théorie quantique des champs. Comme son nom l'indique, la théorie quantique des champs est la combinaison de la mécanique quantique et de la théorie des champs. La mécanique classique est plus un jeu de déterminisme, ce qui signifie qu'avec les informations passées, nous pouvons en dire beaucoup sur l'avenir. La mécanique quantique, quant à elle, est une question de probabilités. L'acte de mesure, en mécanique quantique, altère la réalité des phénomènes physiques. La combinaison de tous les résultats possibles d'une particule est connue sous le nom de fonction d'onde qui peut être comprise comme les propriétés intrinsèques de la particule quantique comme la position, l'impulsion, la vitesse, etc. Un individu ordinaire observe le monde matérialiste mais un scientifique, en particulier, un physicien observe un monde avec de la matière et des champs. L'espace vide, en physique, n'est pas forcément vide. Essayons de le comprendre avec un exemple simple lorsque vous essayez de joindre les pôles similaires d'un aimant ensemble, vous ressentez une sorte de force répulsive. La région entre les aimants est considérée comme vide, mais nous ressentons toujours une sorte de force agissant là-dedans. L'espace considéré comme vide contient en fait un champ magnétique. De même, les espaces vides dans l'univers ne sont pas vraiment vides, ils contiennent des champs. C'est l'idée de base de la théorie des champs. les espaces vides dans l'univers ne sont pas vraiment vides, ils contiennent des champs. C'est l'idée de base de la théorie des champs. les espaces vides dans l'univers ne sont pas vraiment vides, ils contiennent des champs. C'est l'idée de base de la théorie des champs.

Source des images

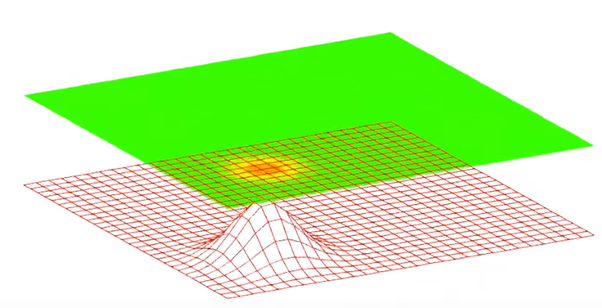
Maintenant, lorsque vous combinez la mécanique quantique et la théorie des champs, cela donne naissance à la théorie quantique des champs qui stipule que partout dans cet univers et à chaque instant du temps, il existe différents types de champs que nous ne pouvons pas voir comme un champ magnétique, un champ électrique , champ gravitationnel, etc. En fait, chaque particule élémentaire a son propre champ comme le champ de Higgs, le champ d'électrons, le champ de quarks, etc. Les physiciens représentent ces champs par des nombres. Nous voyons un ou plusieurs de ces nombres dans chaque point de l'espace. Les champs sont divisés en plusieurs types en fonction du nombre de numéros requis par un champ. Par exemple, le champ de Higgs est un champ scalaire car à chaque point de l'espace il nécessite un seul nombre pour décrire ce champ. Les champs électriques et magnétiques sont des champs vectoriels car ils nécessitent à la fois une amplitude et une direction pour leur description complète. Selon Sir Isaac Newton, le champ gravitationnel est un champ vectoriel alors que selon Einstein c'est un champ tenseur. Lorsque ces champs reçoivent de l'énergie, ils passent à des états d'énergie plus élevés formant une sorte de ridée comme dans l'eau. Ces ondulations ainsi formées sont appelées particules. Par exemple, lorsque des ondulations se forment dans le champ d'électrons, des électrons se forment. De même, les ondulations dans les champs de quarks nous donnent des quarks. Lorsque ces ondulations deviennent silencieuses, les particules correspondantes disparaissent également. Au point où nous donnons l'énergie dans ces champs, la particule se forme à ce point et lorsque cette énergie commence à se répandre à travers le champ, nous disons que la particule se déplace. Pour certains champs, nous devons fournir une grande quantité d'énergie pour produire les particules. Certains champs nécessitent moins d'énergie pour générer la particule. Le principal facteur qui détermine la quantité d'énergie nécessaire à un champ pour produire une particule dépend de la masse de la particule correspondante associée au champ.

Champs quantiques. Source des images

Par exemple, les bosons de Higgs sont beaucoup plus lourds que les électrons. Par conséquent, le champ de Higgs nécessite une énorme quantité d'énergie pour générer ces particules. Nous ne pouvons le faire que dans des accélérateurs de particules comme le Large Hadron Collider. Jusqu'à présent, nous avons compris la génération de différentes particules en termes de champs. Voyons maintenant comment fonctionnent les forces fondamentales selon la théorie quantique des champs.

Les champs existent au même endroit dans l'espace et le temps en raison desquels nous voyons souvent l'échange d'énergie entre et parmi les différents champs. C'est ainsi que les forces fonctionnent et, à cause de ce phénomène, une particule est parfois convertie en une autre. C'est l'une des meilleures théories pour comprendre la nature et la réalité au niveau quantique jusqu'à présent. Il y a encore beaucoup de questions associées à la théorie quantique des champs. Il n'a pas été en mesure d'expliquer l'existence de la matière noire et de l'énergie noire. De nombreux physiciens pensent que la matière noire est également le résultat de l'énergie dans certains domaines que nous ne comprenons pas encore.

Sunny Labh

Merci beaucoup d'avoir lu. Si vous aimez mon travail et souhaitez me soutenir alors vous pouvez devenir membre médium en utilisant ce lien ou m'acheter un café ☕️ . Continuez à suivre pour plus d'histoires de ce genre.

Before Big Bang

 

What Existed Before The Big Bang?

Georges Lemaitre lecturing at a University. Source: unknown

In 1927, Georges Lemaître, a Belgian priest, mathematician, astronomer and professor of theoretical physics published a report in the Annales de la Société Scientifique de Bruxelles (Annals of the Scientific Society of Brussels) under the title “Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extragalactiques” (“A homogeneous Universe of constant mass and growing radius accounting for the radial velocity of extragalactic nebulae”), a paper that was going to make him internationally recognized in the scientific as well as the religious community.

The paper provided significant insights into the ‘expansion of the universe’ which Lemaitre derived from the solutions of Einstein’s general relativity. The publication in which the report was published wasn’t much recognizable at the time. However, in 1931, physicist Arthur Stanley Eddington translated Lemaitre’s paper in English. He did not include Lemaitre’s estimation of the ‘Hubble’s constant’ though for reasons that were unknown for quite a long time. Lemaitre observationally estimated the value of the Hubble’s constant at the time but for some reason it was not published in the translation. Edwin Hubble provided the accurate constant value two years later after Lemaitre’s publication.

Physicist and popular science author Mario Livio reported in the year 2011:

Lemaître omitted those paragraphs himself when translating the paper for the Royal Astronomical Society, in favour of reports of newer work on the subject, since by that time Hubble’s calculations had already improved on Lemaître’s earlier ones.

When Lemaitre presented his ideas to Einstein, he did not quite accept it and said “Vos calculs sont corrects, mais votre physique est abominable” meaning:

Your calculations are correct, but your physics is atrocious

Lemaître was then invited to London to participate in a meeting of the British Association on the relation between the physical universe and spirituality where he proposed that the universe expanded from an initial point, which he called the “Primeval Atom”. He developed this idea in a report published in Nature. Lemaître’s theory appeared for the first time in an article for the general reader on science and technology subjects in the December 1932 issue of Popular Science. Lemaître’s theory became better known as the “Big Bang theory,” a picturesque term playfully coined during a 1949 BBC radio broadcast by the astronomer Fred Hoyle.

Albert Einstein and Georges Lemaitre

What is the Big Bang Theory?

The Big Bang hypothesis states that all of the current and past matter in the Universe came into existence at the same time, roughly 13.8 billion years ago. At this time, all matter was compacted into a very small ball with infinite density and intense heat called a Singularity. Suddenly, the Singularity began expanding, and the universe as we know it began. The first atoms are thought to have formed when the universe was around 400,000 years old. Before that, the universe was simply too hot and too energetic to let atomic nuclei capture electrons. The first stars sparkled into life, cosmologists believe, about 250 million years after the Big Bang, and the first galaxies shortly after that.

Crucially, the theory is compatible with Hubble–Lemaître law — the observation that the farther away a galaxy is, the faster it is moving away from Earth. Extrapolating this cosmic expansion backwards in time using the known laws of physics, the theory describes an increasingly concentrated cosmos preceded by a singularity in which space and time lose meaning.

Image: Getty Images

The religious/mythological view

According to Boshongo people of central Africa, in the beginning there was only darkness and water. Along with those two elements existed a god named Bumba. Bumba, one day, vomited out of stomachache and spitted the sun. The sun dried up some water leaving land. He vomited some more spitting moon, stars and so on. According to the old testament, god created Adam and Eve only six days into creation. The Qur’an says that “the heavens and the earth were joined together as one unit, before We clove them asunder” . Following this big explosion, Allah “turned to the sky, and it had been (as) smoke. He said to it and to the earth: ‘Come together, willingly or unwillingly.’ They said: ‘We come (together) in willing obedience’. Thus the elements and what was to become the planets and stars began to cool, come together, and form into shape, following the natural laws that Allah established in the universe. The Qur’an further states that Allah created the sun, the moon, and the planets, each with their own individual courses or orbits. “It is He Who created the night and the day, and the sun and the moon; all (the celestial bodies) swim along, each in its rounded course” For Hindus the universe was created by Brahma, the creator who made the universe out of himself. After Brahma created the world, it is the power of Vishnu which preserves the world and human beings.

God rests with his creation. Julius Schnorr von Carolsfeld 1860

What existed before the big bang?

Before we proceed to answer this question, it’s important to understand the fact that big bang theory is, so far, the most widely accepted theory of beginning which is consistent with the working mathematics. Big bang ‘explosion’ is considered to be the beginning of space and time itself. Thus, there is nothing before the initial moment of the universe’s rapid expansion. Theoretically speaking, the Big Bang took place at no place and at no time. Thus, there is nothing before the initial moment of the universe’s rapid expansion. The question is similar to the question of “What happens if you move two objects closer together than zero distance.”

There’s a very interesting analogy that might help us understand the ‘prior-to-big-bang’ universe. Pick the smallest real number that is bigger than 0. Somehow one can always pick one that is smaller than yours. If you pick 0.0001, one can pick 0.00005. In fact, one can always just take the half of your number, and that will be a smaller one. Hence asking what is the smallest number greater than zero does not make any sense. There is no smallest number that is bigger than 0. Big Bang is something similar. There was no first moment. Time itself came to existence with it, and we cannot point to the earliest moment. As in the example above — we can always have a moment earlier than a particular other. We call that first missing moment a singularity.

Here’s a thought: What if our universe is but the offspring of another, older universe? Some astrophysicists speculate that this story is written in the relic radiation left over from the Big Bang: the cosmic microwave background (CMB).

The Conformal Concyclic Cosmology Hypothesis

Unexpected hot spots in the cosmic microwave background (CMB) could have been produced by black holes evaporating before the Big Bang. So says a trio of scientists led by mathematical physicist Roger Penrose in a paper presenting new evidence that our universe is just one stage in a potentially infinite cycle of cosmic extinction and rebirth.

CMBR mapped by COBE and WMAP

Penrose, based at the University of Oxford , has developed a rival theory known as “conformal concyclic cosmology“ (CCC) which posits that the universe became uniform before, rather than after, the Big Bang. The idea is that the universe cycles from one aeon to the next, each time starting out infinitely small and ultra-smooth before expanding and generating clumps of matter. That matter eventually gets sucked up by supermassive black holes, which over the very long term disappear by continuously emitting Hawking radiation. This process restores uniformity and sets the stage for the next Big Bang.

CCC hypothesis (left) and Nobel prize winning physicist Roger Penrose (right). Credits: National portrait library

The theory is a fascinating and imaginative alternative to inflation, but the data doesn’t support it. If Penrose’s CCC hypothesis is correct, we should also be able to see some left-over information from the previous aeon in the cosmic microwave background around us. The data, however, speaks a different story. Let’s leave this topic for the upcoming article.

Thank you so much for reading. You may check out my other articles at 

Physics History

. If you like my work and want to support me then please sign up to become a medium member using this link or else, you can buy me a coffee ☕️

How Symmetry Shapes Physics

 

Noether’s Theorem: How Symmetry Shapes Physics

Jason Segall

In 1915, mathematicians David Hilbert and Felix Klein came to Emmy Noether with a problem [1]. Einstein had published the field equations for his general relativity earlier that same year, and there seemed to be a worrying hole in the theory. Under certain circumstances, one of the most fundamental principles of physics was violated. Energy was not conserved.

Emmy Noether was born in 1882 to a wealthy Jewish family in Bavaria [1]. Her father, Max Noether, was a maths professor known for his studies in algebraic geometry [2], but it was languages which originally interested Emmy [1]. It was only after having qualified as a teacher of English and French that she began studying mathematics at university level, albeit unofficially as women were not allowed to matriculate at German universities at the time [1].

This rule was changed in 1904, and, by 1907, Noether had been awarded her doctorate. Her thesis was in the realm of abstract algebra, specifically on invariants — properties of functions or groups of functions which remain unaltered when the function is transformed [3] — and it was in this area of mathematics that she swiftly built her reputation, to the extent that she was invited to join the German Mathematical Society in 1909 [1].

It was as an expert in invariants that Hilbert and Klein came to Noether in 1915. If anyone could find a way to plug the gap in the theory, it would be her. They were not wrong. Noether’s resolution led to one of the most elegant and powerful results in theoretical physics.

A photograph of Emmy Noether before 1910. Published by the Mathematical Association of America

A statement of Noether’s theorem is:

If the Lagrangian of a system has a continuous symmetry, then there exists an associated quantity which is conserved by the system, and vice versa.

Let’s unpack this statement. First, a conserved quantity is any property of a system which remains constant over time. For example, if I putt a golf ball, then the mass of the ball doesn’t change in the time between when I strike the ball and when it (hopefully) goes in the hole. Thus, the mass of the ball is a conserved quantity of the system.

Conversely, the speed of the ball changes over time, whether through friction with the grass or the contours of the green. The velocity of the ball is not a conserved quantity in this case.

Next is the idea of a continuous symmetry. Think back to primary school, and the idea that a square, say, is rotationally symmetric when rotated by an angle of 90°. This means that, when we rotate a square by 90°, the final state looks exactly like we hadn’t done anything at all. This, however, only holds for certain angles. If we were to instead rotate by 45°, the final state would be markedly different to the original orientation. So, we say a square has discrete rotational symmetry.

Now imagine performing the same process on a circle. This time, however, no matter what angle we rotate the circle by, the circle always looks exactly the same, even if that angle is a tiny fraction of a degree. This means the circle has continuous rotational symmetry.

The rotational symmetry of a square. We can see that this symmetry is discrete, since the square only looks the same for certain angles of rotation. Produced using Wolfram Mathematica

Lastly, what is the Lagrangian of a system? To describe the Lagrangian, we must first understand another of the fundamental ideas in physics: The Principle of Least Action, or PLA as physicists affectionately know it. In effect, this states that the universe is lazy. Physical systems proceed in a manner which minimises the “effort” necessary for the evolution of the system from one state to another. We quantify this “effort” as what is known as the action of the system.

For example, when I hit my putt earlier, in broad terms the physical system evolved from the “ball at my feet” state to the “ball in the hole” state. There’s nothing stopping the ball from travelling the 10 feet from my feet to the hole via Timbuktu, except that the action of the system would be far larger than if the ball had followed the trajectory which we would expect. This latter path, the physical trajectory, is the trajectory which minimises the action. This is the PLA at work.

How does this relate to the Lagrangian? The Lagrangian describes how the energy of the system should change during a process to minimise the action of the system. By examining how it behaves over space and time in a set of differential equations known as the equations of motion, we can determine how the system evolves from one state to another according to the PLA.

A Golf ball about to enter the hole. The path the ball travels is that which minimises the action of the system, and can be found from the Lagrangian

So, back to Noether’s theorem. What does it mean for a Lagrangian to have a continuous symmetry? If, when transformed continuously along some coordinate, the Lagrangian for a system is unchanged, then the system is said to be continuously symmetric about that coordinate.

So, consider a classic physics exam question: the collision of two identical balls on the x-axis. Assuming no friction or air resistance, it can be easily shown that dynamics of the system depend only on the difference between the positions and velocities of the balls, and not on their absolute values.

If we translate both balls by the same arbitrary amount in the x direction, then the difference in position and velocity of the two balls is unaltered. Thus, the system must behave in the same way as if it hadn’t been moved at all. Since this behaviour is encoded in the Lagrangian, this means that it also cannot be altered by a translation in the x direction. This means that the Lagrangian for this system must be continuously symmetric in the x direction!

Noether tells us that this symmetry implies a conserved quantity, and in the case of this translational symmetry, the conserved quantity is momentum [4]. This is the origin of the law of conservation of momentum! The very tool we use to solve problems related to this scenario comes about as a consequence of the symmetries of the Lagrangian describing the system.

Similarly, if a Lagrangian for a system is rotationally symmetric, then angular momentum is conserved in the system [4]. The Lagrangian describing the gravitational force of planets is rotationally symmetric, so angular momentum is conserved in the orbits of planets, for example. Even electric charge is conserved due to a symmetry, this time the slightly more esoteric idea of local phase invariance of the wavefunction, the details of which deserve their own article.

A table showing some common symmetries and their associated conserved quantities. From [4].

This is fantastic, but how does it solve our problem in general relativity? Recall that Hilbert and Klein had realised that under certain circumstances, energy was not conserved by general relativity. We know that energy is usually conserved, so, using Noether’s theorem, what symmetry is invoked by conservation of energy? The answer is time. If a system is symmetric under time translations — if the Lagrangian of the system does not explicitly depend on time — then it must conserve energy [4]. And this, Noether realised, was the answer.

Time in general relativity is not an absolute quantity like it is in the Newtonian world, it flows and warps as spacetime is curved by the contents of the universe. Time translation symmetry only holds in general relativity under certain special circumstances, namely in the case of a flat or asymptotically flat spacetime, so, in general, energy need not be conserved!

So, through a combination of her expertise in abstract algebra and a fantastically analytical mind, Noether not only plugged a hole in one of the most important theories of the 20th century, but brought to light a truly fundamental idea in theoretical physics. Her theorem underlies a huge amount of the physics which we encounter daily, both in the classroom and in the world at large.

And yet, Noether is, for the large part, unknown. This is a woman who was described by Einstein himself as

“The most significant, creative, mathematical genius thus far produced since the higher education of women began.” [5]

Despite this, she never occupied a permanent faculty role. Hilbert was forced to advertise her lecture courses under his own name at Göttingen, such was the opposition to female academics in the university hierarchy at that time [1]. With the rise of the Nazis in 1933, she moved to the US, and was due to begin a position at Princeton alongside Einstein before her sudden death from cancer in 1935 [1]. We can only imagine what might have been discovered had fate allowed their genius to combine.

References

[1] J. O’Connor and E. Robertson, “Emmy Amalie Noether,” November 2014. [Online]. Available: https://mathshistory.st-andrews.ac.uk/Biographies/Noether_Emmy/. [Accessed 3 June 2020].

[2] J. O’Connor and E. Robertson, “Max Noether,” December 2008. [Online]. Available: https://mathshistory.st-andrews.ac.uk/Biographies/Noether_Max/. [Accessed 3 June 2020].

[3] Encyclopedia of Mathematics, “Theory of Invariants,” [Online]. Available: https://encyclopediaofmath.org/wiki/Invariants,_theory_of. [Accessed 3 June 2020].

[4] D. Feng and G. Jin, Introduction to Condensed Matter Physics, vol. 1, Singapore: World Scientific Publishing, 2005, p. 18.

[5] D. Radford, On Emmy Noether and Her Algebraic Works, Governor’s State University, 2016.

Jason Segall