Euler’s Formula for Convex Polyhedrons
Below is a famous and beautiful result from Mathematics known as Euler’s (pronouced ‘Oy-luh’) Formula.
A polyhedron is a solid whose surface consists of a number of faces, all of which are polygons, such that any side of a face lies exactly on another face.
Here is a polyhedron, called the Dodecahedron, made up of twelve pentagons.

Let's take a look at a few more examples, the Cube, the Tetrahedron and a Fourth Shape comprised of square and triangle faces.

Let’s also write down the number of V vertices , E edges and F faces the four shapes have and we notice the following:
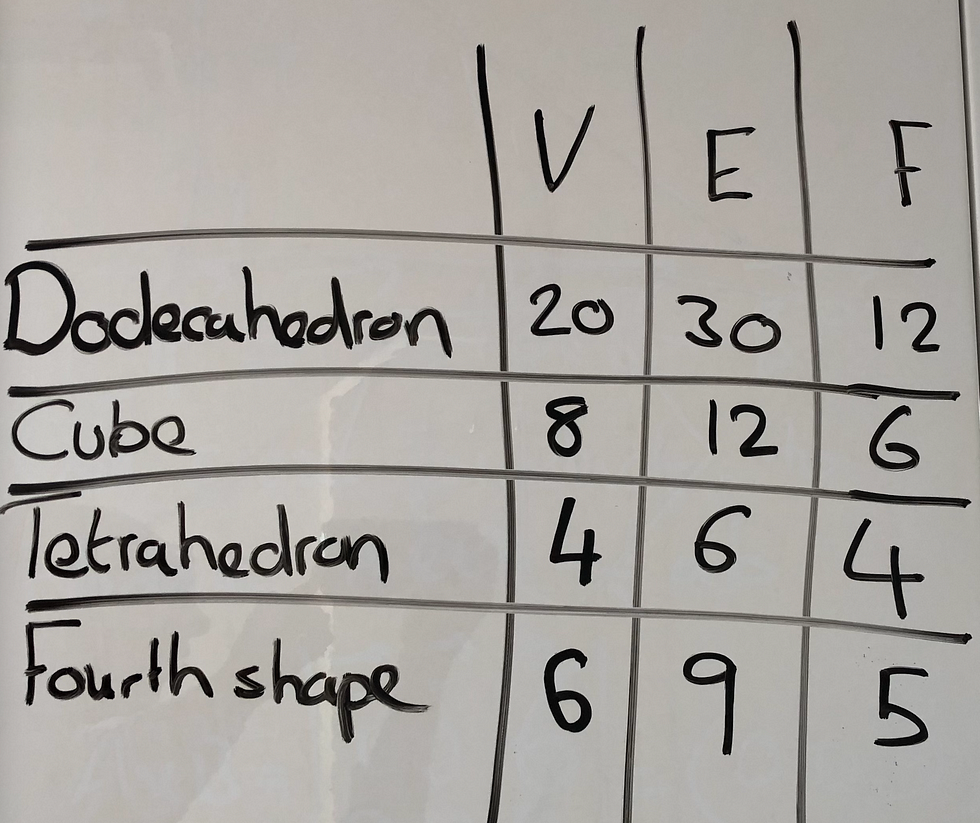
The formula V - E + F = 2 seems to hold. It is a remarkable fact that this is in fact true for all convex polyhedrons.
We can state the theorem explicity here.
Theorem A
For a convex polyhedron with V vertices, E edges and F faces we have V - E + F = 2
By convex, we mean a polyhedron, where taking a straight line between any two vertices will lie wholly inside the polyhedron.
All of the above are convex polyhedrons, however imagine a Cube with a smaller Cube omitted from the centre, this shape has 16 vertices, 24 edges and 12 faces where V - E + F = 4 and not 2.
We will prove this theorem below by thinking about these shapes in two dimensions rather than 3. Just about anyone could follow the logic.
Proving Euler’s Formula
First we need a definition and another theorem to help us prove the result.
Definition: A plane graph is a figure in two dimensions consisting of points (vertices) and edges joining these vertices such that no two edges cross each other. A plane graph is said to be connected if we can get from any point (vertex) to another by going along a path of edges.
For example, here are some connected plane graphs.
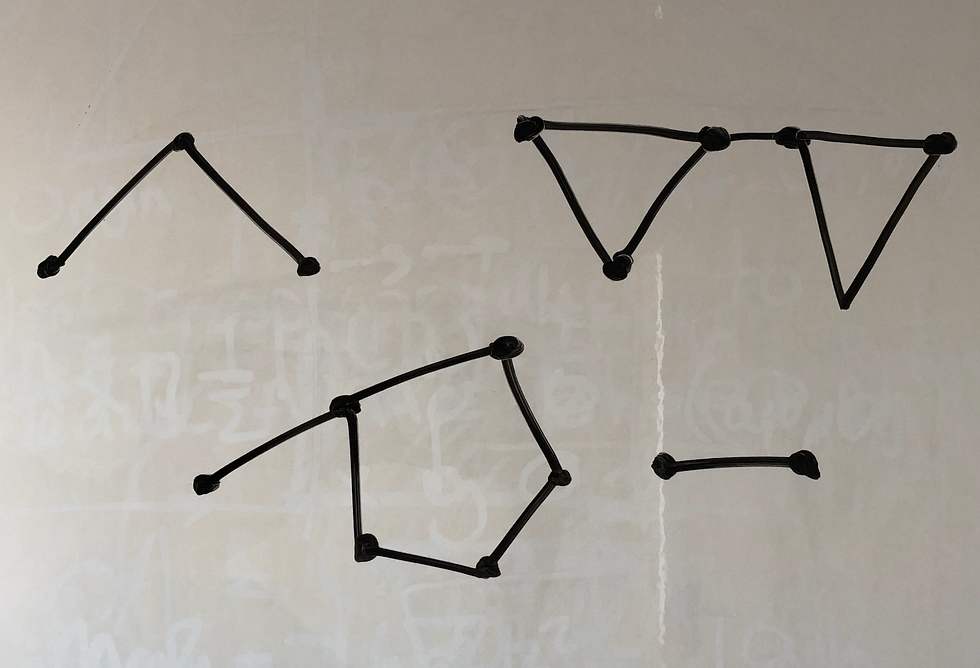
Notice, it appears to be the case that V - E + F = 1. Indeed, we will prove below (Theorem B) that for all connected graphs this formula will hold.
This result helps us to prove Theorem A above, since if we put our eyes very close to one face of the Cube or the Tetrahedron or the Foruth Shape above and drew it on a piece of paper then we would draw something like this.

These are all connected graphs. We are saying then, that all convex polyhedrons can be viewed as connected plane graphs (think with a face removed) and so if V - E + F = 1 for all connected plane graphs then V - E + F = 2 for all convex polyhedrons.
It remains for us to prove this result about connected plane graphs.
Theorem B
For a connected plane graph with V vertices, E edges and F faces we have V- E +F = 1
Proof: First consider plane graphs with only 1 edge, in fact, there is only one such graph which we can clearly imagine to have 2 vertices, 1 edge joining these vertices and 0 faces. Our formula above definitely holds since 2 - 1 + 0 = 1.
However, we want this to be true for any connected plane graph with any number of edges.
Now lets use a technique called Induction in Mathematics which says that if we know a statement P(k) is true for some number k and we can show that P(k+1) is also true then this must mean that P(n) is true for all numbers n which are greater than k.
This is like a domino effect, imagine pushing one domino over and watching all of them fall.
Our statement P(k) could be V - k + F = 1 for all connected plane graphs with k edges.
Note that P(1) is definitely true (shown above), now lets says P(k) is true, we want to prove that P(k+1) is true.
Consider P(k+1), then any connected plane graph with k+1 edges will either have a face or will not have a face.
In the case it does have at least one face, then we can take a face and remove an edge from it. This new connected plane graph has k edges as opposed to k + 1, V vertices and F - 1 faces.
We can then use the idea that P(k) is true and apply our formula to get V - k+(F - 1) = 1. However this can be rewritten as V - (k+1) + F = 1 which is precisely the formula we required for P(k+1) to be true when the graph has at least one face.
In the case it does not have a face then it must have an end vertex, that is, a vertex which has an edge to one side but not the other.
If we remove this end vertex, and it’s accompanying edge, then we get a new connected plane graph with V - 1 vertices, k edges and 0 faces.
We can then use the idea (again) that P(k) is true and apply our formula to get (V - 1) - k + 0 = 1 which can be rewritten as V - (k + 1) + 0 =1 which is precisely the formula we required for P(k+1) to be true when the connected plane graph has 0 faces.
Theorem B now follows and so Theorem A must also hold true.
A closing remark for those not familiar with Mathematics is that it’s normal for Mathematicians to think about problems in different ways where it might be easier to prove results.
Here we reimagined the challenge around convex polyhedrons as a problem about connected plane graphs. If you are interested in an application of this result, see my other write-up Known since Antiquity: The Platonic Solids.
Sundip Tailor
References
Above proof found in Chapter 9 of ‘A Concise Introduction to Pure Mathematics’, First Edition By Martin Liebeck (Chapman & Hall/CRC Mathematics)