
The Unattainable Speed of Light
How does special relativity add velocities? Welcome to the world where 1 + 1 is not quite 2.
A letter poured in
I received a letter with some questions about special relativity. Here is a part of that letter:
…let’s say we hypothetically were able to send a space ship across space at the speed of light minus 5 mph. Couldn’t a person run from the back of the space ship to the front at 10 mph? — Luke Copko
The implication is that the runner has now broken the light barrier. That’s a no-no in the world of special relativity.
An observer (call him Luke) is on Earth, witnessing this whole scenario. Let’s have another observer (call her Leia) sitting aboard the ship, monitoring the dilithium. Won’t the runner (call him Anakin) be moving at 5 mph above the speed of light?
Here’s what we might expect from Luke’s frame of reference.
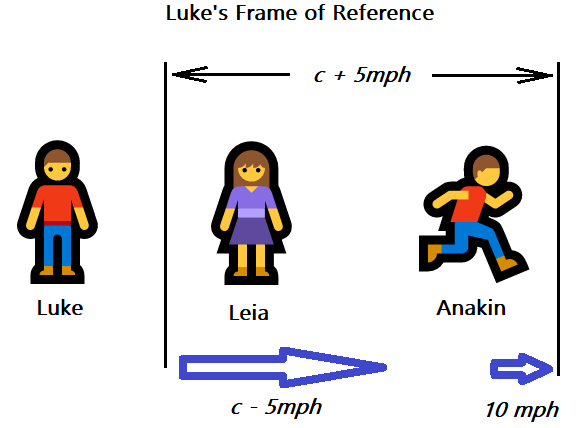
How do we explain this apparent breach of relativistic protocol?
Now consider Leia’s frame of reference. Wouldn’t she see Anakin moving one way at 10 mph, and Luke moving the other way at 5 mph short of the speed of light? That also totals 5 mph above the cosmological speed limit.
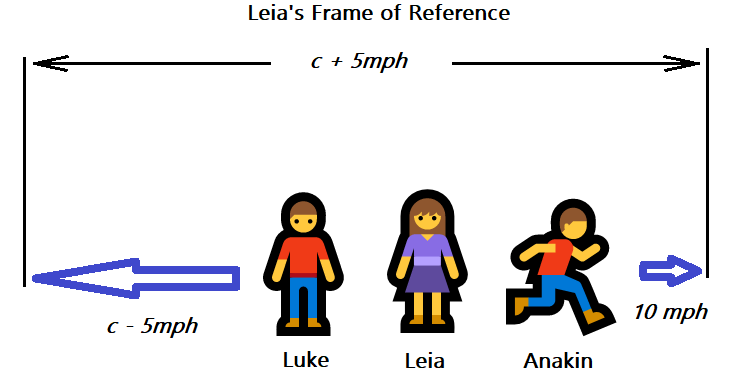
It turns out that this arrangement is legal. Why is one okay and the other forbidden? Why is special relativity so fickle?
The two commandments of relativity
The theory of special relativity has two rules:
- All inertial reference frames are equivalent.
As long as that space ship is moving in a straight line at a constant speed, it is an inertial reference frame. Leia measures the Anakin’s speed to be 10 mph. That’s a valid measurement. Leia also measures Luke’s speed on Earth in the opposite direction: 5 mph short of the speed of light.
2. The speed of light is the same in all inertial reference frames.
Suppose Anakin fires a pulse from a laser. He will measure the pulse leaving the laser at 186,000 miles per second. Won’t an Leia measure the pulse moving at an additional 10 mph? Won’t Luke measure it to be moving at twice light speed plus 5 mph? Nope. Everyone measures the speed of the laser pulse to 186,000 miles per second.
The second axiom may be the harder to swallow. Maxwell’s equations provide the theory behind Rule #2. Experiment provides the physical evidence. We won’t delve into it any further here. We will, however, examine the implications of Rule #2.
Let’s have the space ship travelling at ⅘ light speed. Within, Anakin clips along at ⅖ light speed. We’ll have V be his speed with respect to Luke. Here’s what we might expect:
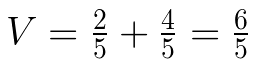
We know from previous articles that motion messes with time and distance. What will it do to Anakin’s velocity?
To check V, we will define an event upon which both Luke (on the ground) and Leia (on the ship) can agree. The trouble begins when we compare two events separated by distance or time.
The instant Anakin begins his run, he fires a light pulse from his laser. The far end of the ship reflects the pulse back toward Anakin. When the pulse strikes him, he drops on the spot. (Don’t worry. He’ll be okay.)
Where is Anakin?
Leia’s frame of reference
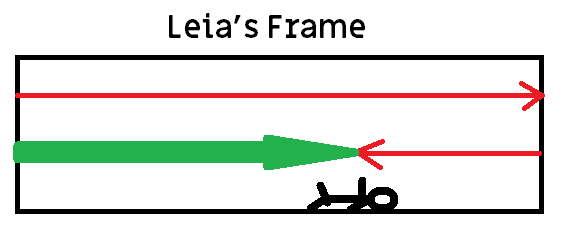
The thick arrow shows Anakin’s motion. The thin arrows are the light beams. The light travels much further than does Anakin. How far does he get? Half way across the ship? A quarter of the way? Wherever he is, Luke and Leia will agree.
We’ll calculate this distance for both frames of reference. Then we’ll equate the two expressions and see what happens.
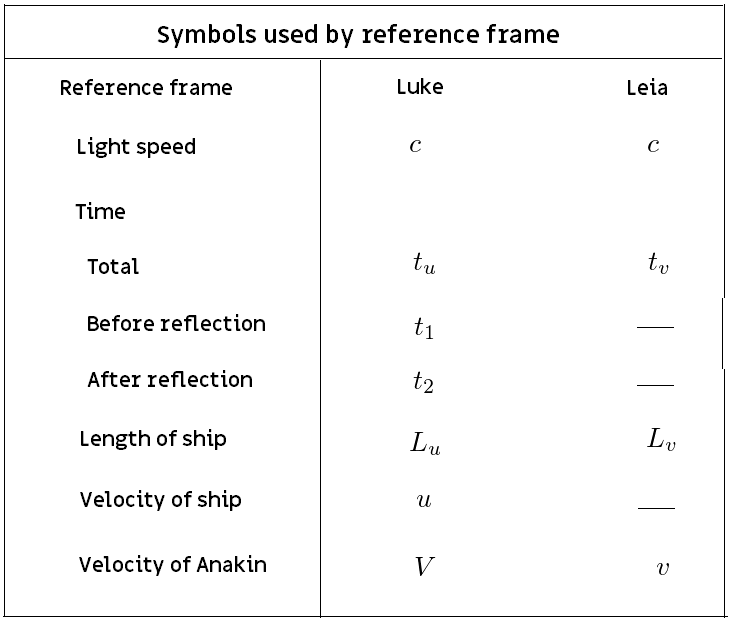
The speed of light is our standard. We can define the distance travelled by the light in Leia’s frame as our unit length. That is the total length of the two thin arrows. Anakin was running at ⅖ light speed so the length of the thick arrow is ⅖. How long is the ship? The three arrows together have a total length of 1⅖. The length of the ship is half that total:
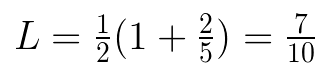
What fraction of the ship’s length did Anakin travel? Take his distance and divide it by the length of the ship.
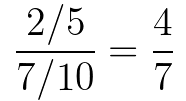
Anakin makes it just over halfway across the ship. If we marked the floor off in 7th’s, he’d collapse at mark #4. Neither Luke nor Leia will dispute this.
Luke’s frame of reference
How does this play out for Luke?
We need not assume anything about how the times, distances and velocities in Leia’s frame compare to Luke’s frame. But they will have to agree on two measurements:
- the speed of light, c
- the proportion of the ship's length travelled by Anakin (4/7 in our example)
Luke measures Anakin running at some speed, V, which intuition tells us must be 1⅕ light speed. He also measures a laser pulse travelling at — according to Rule #2 — the speed of light. Finally, he measures the ship’s speed to be ⅘ light speed.
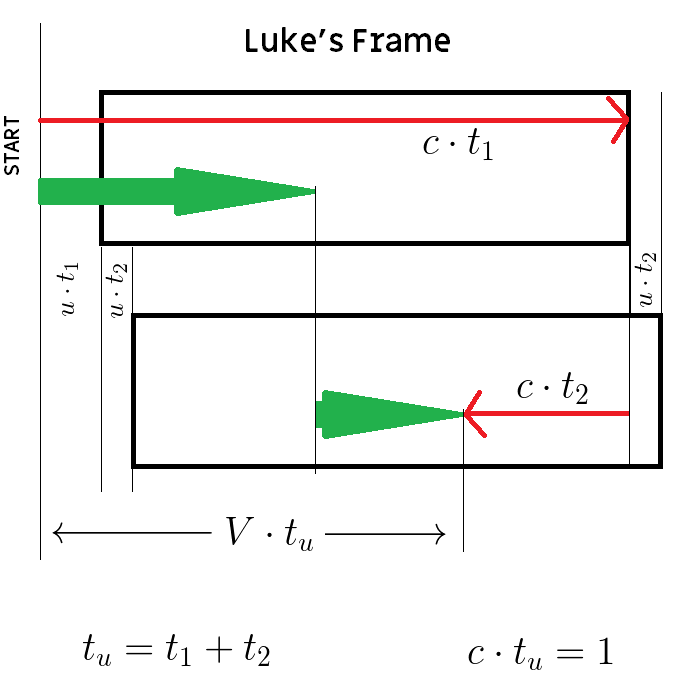
First, the laser makes the trip to the far end of the ship. It has a little further than the length of the ship to travel because the ship is moving. Anakin has run ⅖ of that distance. Because the ship has also advanced, he is less than ⅖ of the way across.
At the end of the journey, Anakin has travelled a distance of V·tᵤ with respect to Luke. Here, tᵤ is some time as measured by Luke.
Although Anakin travels a distance of V·tᵤ, the ship has advanced a distance of u·tᵤ, where u is the speed of the ship. This is how far Anakin ends up from the rear of the ship:
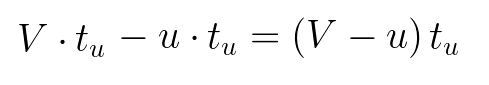
In our example, the ship’s speed, u, is ⅘ light speed. The thing we want to find out is V, and the time variable, tᵤ, will eventually disappear. Once we have the length of the ship, we hope to show:
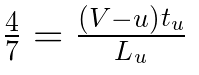
This is the distance along the ship divided by the length of the ship, as measured by Luke.
In the calculations below, it may help to print out the diagram of Luke’s reference frame. You can then refer to it as you follow each step of the argument.
Anakin’s position is the same in both frames
Recall how we worked this out for Leia’s frame of reference. She measures Anakin’s speed as ⅖ light speed. We can generalize the previous calculation by representing Anakin’s speed with the variable v.
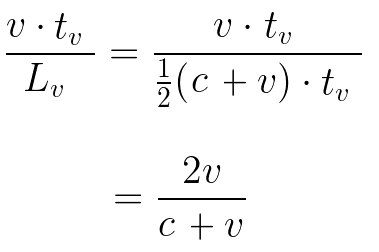
We need an expression for the length of the ship in Luke’s frame. This is the distance the light travels to the end of the ship, less the distance the ship moves in that time.
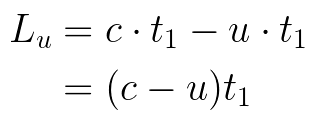
The time, t₁, presents a problem. We need the times to eventually cancel, so we want only one time variable, tᵤ. First, we express in terms of tᵤ.
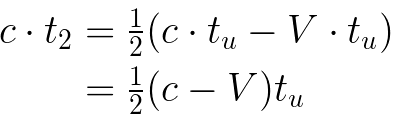
Next, we use the fact that tᵤ=t₁+ t₂ to find an expression for t₁.
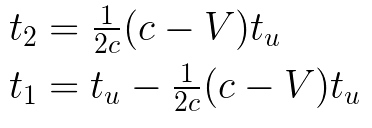
We insert our t₁ into the above expression for Lᵤ and tidy it up a bit.
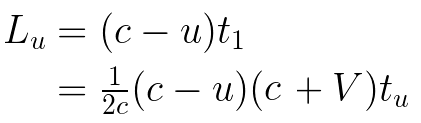
We divide the distance Anakin travels across the ship with the length of the ship. This gives us a distance in terms of ship length. What proportion of the ship did Anakin cross?
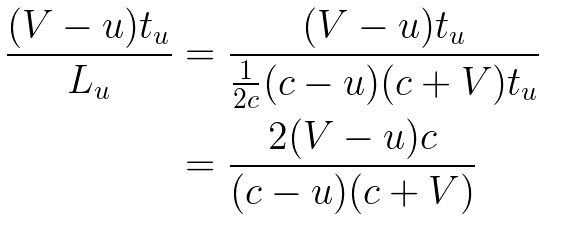
That proportion is frame independent.
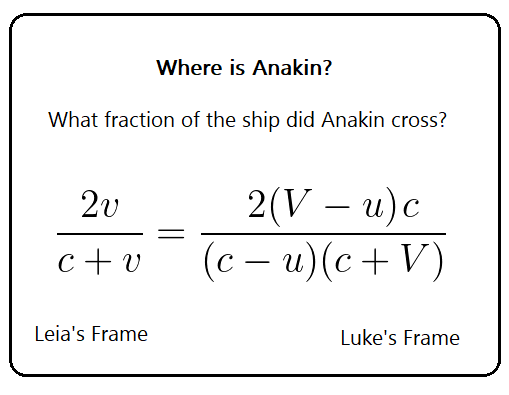
How fast is Anakin moving away from Luke?
We are left with the tedium of isolating V. This will give us the sought-after expression for Anakin’s speed according to Luke.
Cross multiply numerators with denominators.
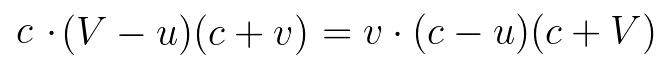
Expand.
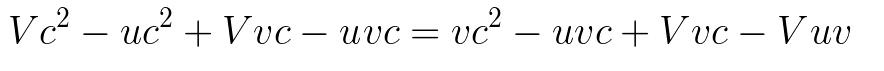
Bring the V terms to the left, and cancel equivalent terms.
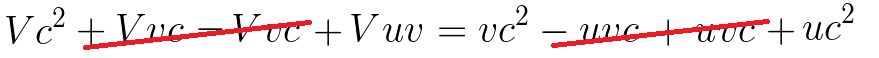
Isolate V.
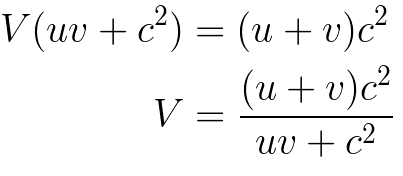
Tidy up the result by dividing top and bottom by c².
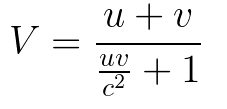
If we are consistent about expressing velocities as fractions of light speed, c=1. We can eliminate c from the expression.
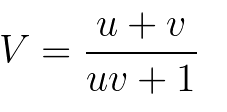
Plug in the values from our example and…
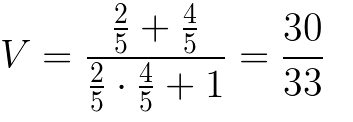
In Luke’s frame, Anakin chugs along at about 90% light speed.
We do add velocities. But then we apply an adjustment. That means dividing by 1 + uv. When u and v are small — which they usually are, uv is very close to 0. The adjustment is negligible.
We must be careful about mixing our reference frames. The distance between Luke and Anakin is increasing at 1⅕ light speed with respect to Leia, but not with respect to each other.
What about Luke and Anakin together from Leia’s point of view? Why no adjustment? In Leia’s frame, the distance between Luke and Anakin increases at 1⅕ light speed: Anakin at ⅖ to her right; Luke at ⅘ to her left.
We must be careful about mixing our reference frames. The distance between Luke and Anakin is increasing at 1⅕ light speed with respect to Leia, but not with respect to each other.
If Luke fires a light pulse at Anakin, we know it will overtake him. According to Luke, Anakin is moving away at about 90% light speed. Leia will see the pulse approach her at light speed, pass her, and overtake Anakin. Anakin will see it approach him at light speed also.
When we speak of the distance increasing at 1⅕ light speed, the distance isn’t a thing which can carry a signal at a super-luminous velocity. We must carefully select our frame of reference. Nobody is moving at greater than light speed in anyone’s frame.
All is well. God is in his curved space-time heaven.
Sign up for Ravings of a Quarantined Mathematician
By MathAdam
A monthly-or-so-ish overview of recent mathy/fizzixy articles published by MathAdam. Take a look
