This Math Puzzle Looks Hard

Infinitely-sided dice produce a surprising result.

Here’s the challenge. You have three infinitely-sided dice. When you roll one of these dice, you get a Real Number between 0 and 1. So when you roll three of these dice, you get a Real Number between 0 and 3. Capish?

Here’s the question. You roll the three dice. You square the outcome of each die.

What are the odds that the sum of the three squares will be less than or equal to 1?

These examples should clarify:

Infinitely-sided dice produce random Real Numbers between 0 and 1. Examples shown are all Rational Numbers, but this would be extremely unlikely because…um… Math.

In the first example, we roll 0.98, 0.35 and 0.72. (We’ll stick to rational numbers to keep things clean.) The sum of the squares (0.98²+0.35²+0.72² =1.6013) is greater than 1, so this is a fail.

In the second example, we roll 0.89, 0.21 and 0.37. The sum of the squares (0.89²+0.21²+0.37² =0.9731) is less than 1, so this is a win.

Now, roll those magical mathematically perfect dice. How likely are you to win?

So you don’t accidently scroll down and see a spoiler, I will place this photo of my cat here.

Proof that if you leave out bedding, it will spontaneously generate a cat.

Solution

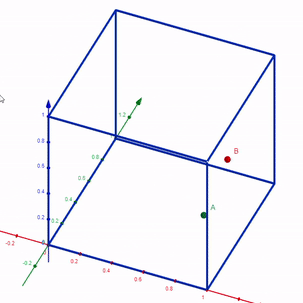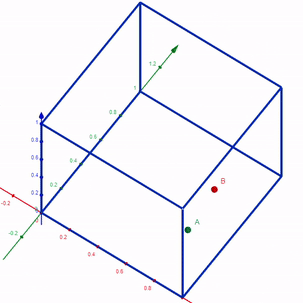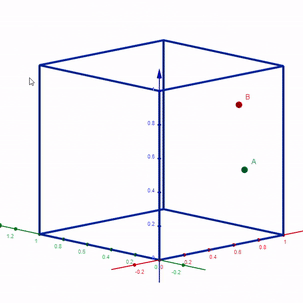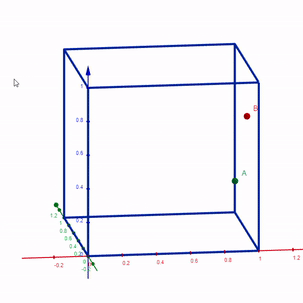
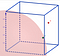
Represent the space of possible outcomes within a 3-D cube.

Each point in this 3-D space takes the outcome of the dice as its x, y, z coordinates. Point A is (0.89, 0.21, 0.37). Point B is (0.98, 0.35, 0.72).

Now, let us include our condition: x²+y²+z²≤1.

Our condition — that the sums of the squares be less than 1 — gives us the set of points on the surface of, or contained within, a sphere of radius 1.

We can reframe our question as follows.

Given a random point within a 1×1×1 cube, what is the probability that it will fall within a sphere of radius 1, with a centre at one of the cube’s corners?

We need the volume of that chunk (an eight) of the sphere, and the volume of the cube. Divide one by the other, and we’re done.