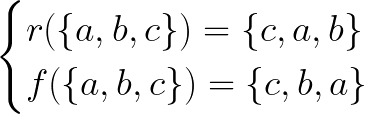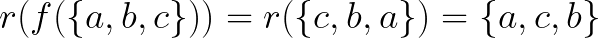Théorie des groupes pour débutants : une approche intuitive
Qu'est-ce qu'une symétrie exactement ?

Lorsque nous parlons des mathématiques en termes de beauté, de symétrie et de puissance, nous laissons souvent de côté exactement ce que sont ces choses. Vous êtes-vous déjà demandé ce qu'est exactement une symétrie ?
(traduction automatique)
Dans cet article, je décrirai l'étude mathématique connue sous le nom de théorie des groupes, qui est à la base des domaines connus sous le nom d'algèbre abstraite et d'algèbre moderne. Ne vous laissez pas décourager par la formulation, ce n'est finalement pas si difficile.
Cet article est écrit pour toute personne ayant même une connaissance de base de la géométrie et de l'algèbre depuis le lycée. Ce n'est pas grave si vous avez tout oublié : nous recommencerons depuis le début ! Nous allons construire le sujet à partir de zéro; Donc, tout ce que vous devez savoir, ce sont des faits de base sur les ensembles et les nombres. Mon principal conseil pour commencer est de ne pas trop penser aux choses ; rien n'est plus que ce que dit la définition. Ce sont des mathématiques vraiment simples.
Feuille de route de l'article :
- Symétries du triangle intuitivement
- Définition du groupe
- Quelques faits sur les groupes, et quelques exemples de groupes
- Définition d'une géométrie et d'une symétrie (!!)
Symétries du Triangle
Nous commencerons par les symétries du triangle, comme moyen approximatif de comprendre la terminologie à venir. Tout ce que nous allons faire est d' affiner nos significations à partir de la géométrie de base.
Définition 1 - Triangle : Un triangle est constitué de trois points uniques dans un plan ou de la zone délimitée par trois lignes uniques dans le plan.
Définition 2 - Triangle équilatéral : On dit qu'un triangle est équilatéral si ses trois côtés ont la même longueur.
De la géométrie de base, nous pouvons dire que tous les angles internes sont également les mêmes. Euclide construit le triangle équilatéral de la manière suivante :

Étant donné que les deux cercles partagent un rayon et que les trois points se trouvent sur les deux cercles, la distance entre les deux doit être la même. Nous savons donc que ceux-ci doivent exister sous une géométrie assez normale. Plus sur ce que cela signifie plus tard (retenez cette pensée!) .
Maintenant, les symétries de ce triangle sont à peu près « que pouvons-nous changer dans le triangle, jusqu'à l'endroit où nous récupérons une copie, et nous ne pouvons pas faire la différence entre cette copie et l'original ? »

Prenons le triangle ABC, donné ici. Nous pouvons soit le refléter avec l'une de ses lignes bissectrices, soit le faire pivoter d'un tiers d'une rotation complète. Écrivons-les comme r pour la rotation et f pour la réflexion ; nous les écrirons par ce qu'ils font aux sommets :



Donc, dans cet esprit, nous voyons qu'il y a exactement 6 résultats que nous pouvons obtenir par ces opérations, car nous pouvons les combiner. Par exemple:


Si nous continuons ainsi, nous pouvons nous convaincre que les symétries du triangle correspondent au réarrangement des lettres ; nous pouvons également nous convaincre que les rotations et les réflexions sont suffisantes pour nous donner tous ces résultats. (Si vous voulez l'essayer, découpez un triangle dans un morceau de papier et essayez chaque combinaison de 2 ou 3 réflexions ou rotations. Faites-en un tableau pour voir où va chaque coin. [voir ci-dessous])
Ainsi, nous finissons par découvrir que le triangle {a,b,c} a un ensemble de rotations et de réflexions qui le laissent inchangé ; ceux-ci sont tous « construits à partir » d'une seule rotation et d'une seule réflexion.

Nous appelons ces symétries, ce qui n'est pas encore tout à fait une bonne explication. Nous écrirons cet engin, le triangle avec ces symétries, comme (T, G) , où
T = {a,b,c} et G = (r, f, r², rf, r²f). Vous pouvez considérer cela comme décrivant les propriétés d'un triangle équilatéral : c'est un ensemble de trois points, où certaines rotations et réflexions (celles de G ) le laissent inchangé. Nous appellerons ces symétries pour l'instant, mais affinons notre définition une fois de plus dans un court instant.
Groupes : quoi et pourquoi ?
Définition 3 - Groupe : Un groupe est un ensemble X, combiné à une sorte de multiplication (notée ab en multipliant a avec b ) telle que
- X est fermé : aucun élément de X ne peut être envoyé en dehors de X par multiplication.
- X a un élément identité : il existe un élément e tel que pour tout x dans X, ex = xe = x .
- La multiplication est associative : a(bc) = (ab)c = abc pour tout a,b,c dans X ; et
- La multiplication a un inverse : pour tout x dans X , il existe un élément y tel que xy = yx = e , et nous notons que ce y est x^(-1).
Un groupe est tout ensemble d'éléments pour lesquels cela est vrai. Maintenant, si vous revenez à notre exemple de triangle, j'ai écrit de manière suggestive que le triangle a été donné par (T, G). Le G, tel que nous le décrivons ci-dessus, est un groupe. Si l'on combine les différentes rotations et réflexions, on récupère une rotation ou une réflexion ; il a aussi une identité, et comme notre tableau l'a montré, chacune de ces rotations ou réflexions a un inverse (il y a, dans chaque ligne du tableau, au moins un e , donc il y a au moins un inverse pour chaque élément). Enfin, il est associatif, comme on peut le vérifier par le même raisonnement.
Dans l'exemple du triangle, nous devons noter que le triangle lui-même n'est pas le groupe, ni les sommets ; plutôt, l'ensemble {a,b,c} est influencé par le groupe de rotations et de réflexions. Ce groupe est connu sous le nom de D3, le groupe dièdre agissant sur 3 objets.
Avant de continuer, respirez profondément et n'y réfléchissez pas trop. Tout ce que nous avons fait, c'est nommer des choses que nous comprenons déjà, ou avec lesquelles nous pouvons au moins jouer à un niveau intuitif. Le « grand saut » est que nous avons séparé ces symétries de la chose sur laquelle elles vivent, et en fait, cela est très précieux, comme nous le verrons.
Exemples et faits
Arithmétique Mod 3
Prenons deux autres exemples simples de groupes. La première est l'arithmétique d'horloge sur une horloge à trois heures :

Sur notre horloge à 3 heures, nous allons définir quelques calculs de base. Prenez 2+1 . Une heure après 2 vaut 0, donc 2+1 = 0 .
De même, 2+2 = 1 et 2 x 2 = 1 . Tout le reste agit « comme d'habitude ».
C'est ce qu'on appelle l'arithmétique modulo 3. Nous allons nous concentrer sur les propriétés d'addition pour l'instant ; sous cet ajout, nous appelons l'ensemble {0,1,2} par le surnom Z3, et sur celui-ci nous agissons avec l'opération +. Il s'agit d'un groupe extrêmement basique, agissant sur cet ensemble extrêmement simple. Un bon exercice pour le lecteur intéressé serait de vérifier que ce cas (Z3, +) est un groupe.
Cela se trouve également être équivalent au groupe formé uniquement par les rotations sur le triangle.
Les nombres rationnels
Prenez n'importe quelle fraction p/q , où p,q ne sont pas 0 . Avec l'opération de multiplication, c'est un groupe. C'est aussi un bon exemple à vérifier ! Ils sont également séparément un groupe sous addition, où 0 est maintenant autorisé pour p (mais pas q ! Indice : les identités sont 1 pour la multiplication et 0 pour l'addition.)
Les rotations du cercle unité par un angle de k
Comme vous l'avez peut-être remarqué ci-dessus, les rotations ont tendance à produire des groupes assez facilement dans le plan (nous en parlerons plus tard). Maintenant, notez que l'ensemble de toutes les rotations, agissant soit sur le plan, soit sur n'importe quel cercle centré à l'origine, sont les deux groupes. (Vérifie ça!)
Propriétés des groupes
Maintenant que nous avons quelques exemples, notons les quelques termes et idées suivants :
- Abélien : si l'opération commute, c'est-à-dire si xy = yx pour tous les éléments de X, alors on dit que le groupe est abélien.
- Sous-groupes : si un sous-ensemble du groupe est toujours un groupe avec la même opération, on dit que c'est un sous - groupe . Un bon exemple est les entiers avec addition, et tout ensemble de multiples de nombres premiers ; comme {…-10,-5,0,5,10,15…} écrit ici comme 5Z (pas le même que Z5 !)
- Ordre de groupe : On dit que le nombre d'éléments dans un groupe est son ordre .
- → Théorème de Lagrange : Si H est un groupe d'ordre fini, et G est un sous-groupe de H , alors l'ordre de G divise l'ordre de H. (On peut refaire un tas de jolis théorèmes sur la théorie des nombres ici !)
- Ordre des éléments/Ordre d'un élément : L'ordre d'un élément g est le plus petit nombre k tel que g^k = e l'identité.
- → Théorème de Cauchy : Si H est un groupe d'ordre fini n , et p est un nombre premier qui divise n, alors H possède au moins un élément d'ordre p .
Ceux-ci nous donnent quelques façons de penser aux groupes comme étant les sortes de structures qui sous-tendent la théorie des nombres et la géométrie. Cela nous amène à la définition finale, qui devrait éclaircir conceptuellement une grande partie de notre langage.
La géométrie du prisme des groupes
Définition 4 - Géométrie : Une géométrie est un couple (S,G) , où S est un ensemble et G est un groupe de transformations.
Cela nous amène à la définition suivante :
Définition 5 - Transformation : une transformation est une fonction T d'un ensemble A vers lui-même, généralement notée T : A → A, telle que tout dans A va vers quelque chose d'unique dans A (un vers un/injectif) , et la sortie de T couvre tout A (sur/surjectif). Une fonction qui est un-à-un et sur est appelée une bijection , et une bijection d'un ensemble à lui-même (qui préserve la structure/action du groupe) est un automorphisme .
Ainsi, une géométrie est un ensemble avec un groupe de fonctions sur lui-même, ou un ensemble avec son groupe d'automorphismes. Celles-ci sont également appelées symétries .
De retour à notre triangle, nous avons un langage que nous avons défini pour mieux comprendre :

Maintenant, étendons nos nouvelles compétences linguistiques !
Ici, toute la géométrie est (S,G) . Le triangle est l'ensemble S = {a,b,c} , avec le groupe d'automorphismes constitué de combinaisons de r et f (on dit qu'il est généré par eux). Nous écrivons ce groupe soit comme G soit comme <r,f>. Ces éléments sont respectivement d'ordre 3 et 2 car r³ envoie a → b → c → a (pour tous les éléments c'est vrai), et f² envoie a → c→ a. (encore une fois, il est vrai que chaque élément est conservé, bien que b soit inchangé). Les combinaisons de r etf sont les symétries du triangle.
Maintenant, last but not least, la grande définition :
Définition 6 - Géométrie Euclidienne : La Géométrie Euclidienne est l'ensemble C des nombres complexes, combiné avec le groupe H des transformations de la forme T(z) = r(z) + b, où z est un nombre complexe et b est un complexe constant.
C'est-à-dire que c'est l'ensemble de toutes les rotations et translations du plan. Voyez si vous pouvez voir pourquoi cela a du sens par vous-même, et j'inclurai quelques liens dans les ressources vers des textes qui explorent mieux cette connexion. Cette exploration est un outil puissant.
Le voilà! Faites-moi savoir dans les commentaires si vous souhaitez que je discute d'autres sujets mathématiques.
Ressources/Autres lectures :
Géométrie et topologie cosmique par Michael Hitchman : https://mphitchman.com/geometry/gct-toc.html
Groupes et symétrie par MA Armstrong : http://chiataimakro.vicp.cc:8880/Mathematics/%E6%95%99%E6%9D%90/UTM-Undergraduate%20Texts%20in%20Mathematics/UTM%20Armstrong%20% 20groupes%20et%20symétrie.pdf
ÉCRIT PAR