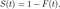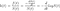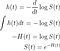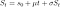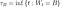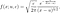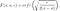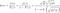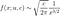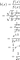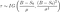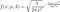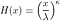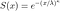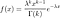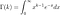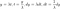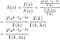11/13/2021

L'effet Lindy

L'effet Lindy : le concept et les mathématiques

Nassim N. Taleb a récemment publié son officialisation de l'effet Lindy . J'ai écrit cet article pour développer ses idées. J'ai utilisé R pour tout tracer et vous pouvez trouver le code ici , mais je fournis également un exemple de code Mathematica.


Eren Asena

(automatic translation)

Un aperçu de ce que je veux discuter:

  1. L'effet Lindy comme fonction de risque décroissante
  2. Mouvement brownien : Lindy fort contre faible
  3. Lindy a-t-il besoin de lois de puissance ? Les distributions de Weibull et Gamma
  4. Intuition pour l' effet de queues : Tuer Lindy avec une barrière réfléchissante
  5. Conclusion

1. Introduction

Pendant de nombreuses années, l'effet Lindy n'a pas eu de formalisation mathématique établie. Le statisticien John D. Cook a souligné en 2012 que Lindy signifiait une fonction de risque décroissante. Cet article a analysé la distribution de Pareto en utilisant la même logique, montrant qu'elle implique l'effet Lindy. J'expliquerai la signification d'une fonction de risque et comment en calculer une ci-dessous. Mais l'idée d'utiliser des fonctions de hasard pour formaliser l'effet Lindy n'a germé que récemment . Il y a quelques années, Taleb a commencé à utiliser le temps d'arrêt du mouvement brownienpour explorer l'effet Lindy. Dans son travail récent que j'ai lié ci-dessus, il a analysé la distribution du temps d'arrêt à l'aide de fonctions de survie et de risque. Il est important de comprendre ce qu'il a fait là-bas. Donc, je vais d'abord décrire les fonctions qui définissent l'effet Lindy. Ensuite, je donnerai un aperçu de ce qu'est le mouvement brownien et pourquoi il est logique de l'utiliser lors de l'étude de Lindy. Après avoir examiné le comportement de Lindy avec le mouvement brownien, nous analyserons quelques distributions de probabilité et verrons que dans certaines conditions, des durées de vie à queue lourde qui ne suivent pas une loi de puissance peuvent toujours montrer l'effet Lindy.

2. L'effet Lindy comme fonction de danger décroissant

Notez que puisqu'il s'agit d'un taux et non d'une probabilité, il peut prendre des valeurs supérieures à 1. Le taux de risque peut être calculé à l'aide de l'expression suivante :

où f(t) est la fonction de densité et S(t) est la fonction de survie. La fonction de survie d'une distribution évaluée à une valeur donne la probabilité que la variable aléatoire soit plus grande que cette valeur, P(T > t). La fonction de survie est donnée par

où F(t) est la fonction de distribution cumulative (CDF). Le CDF donne la probabilité que la durée de vie prenne une valeur inférieure ou égale à un instant donné, donc la fonction de survie est le complément du CDF. L'intégration de la fonction de risque donne la fonction de risque cumulé H(t), qui est le risque de décès cumulé jusqu'à un instant donné t . Notez les identités suivantes qui seront utiles lorsque nous dérivons des fonctions de risque :

La fonction de densité est la dérivée de la CDF, qui est le complément de la fonction de survie, donc lorsque nous différencions la fonction de survie et changeons de signe, nous récupérons la fonction de densité. La dernière identité découle de la différenciation d'un logarithme. Maintenant, nous écrivons la fonction de survie en termes de risque cumulé :

En résumé, la fonction de risque donne le taux de mortalité immédiatement après un point, compte tenu de la survie jusqu'à ce point. Une fonction de risque décroissante signifie que les chances de survie s'améliorent avec le temps - l'effet Lindy. Souvent, une fonction de risque n'est pas monotone mais a une forme en U inversé ; il augmente jusqu'à atteindre une valeur maximale, puis diminue asymptotiquement. Cela signifie que Lindy a besoin de temps pour entrer en action. Taleb a appelé une fonction de risque décroissante de manière monotone « la forte propriété de Pareto ». Par souci de simplicité, appelons-le « Lindy fort » lorsque nous avons une fonction de risque entièrement non croissante et « Lindy faible » lorsqu'elle augmente d'abord puis diminue. Nous allons maintenant examiner quelques exemples de fonctions de risque, en commençant par le temps d'arrêt du mouvement brownien.

3. Mouvement brownien et effet Lindy

Un processus stochastique à valeur réelle W(t) est un mouvement brownien standard (également appelé processus de Wiener) s'il possède les propriétés suivantes (Dahl, 2010) :

  1. Le processus commence à W(0) = 0.
  2. Le processus a des incréments indépendants : pour tout t > 0, l'incrément W(t+s)–W(t) est une variable aléatoire indépendante.
  3. Les incréments sont normaux : W(t+s)–W(t)~N(0, s).
  4. Le processus est continu dans le temps.

Un processus stochastique S(t) est un mouvement brownien arithmétique s'il suit l'équation différentielle stochastique (SDE) :

avec la valeur initiale S(0) = s(0). Cela a la solution

où mu est le terme de dérive et sera négatif dans notre cas. Avoir une dérive négative signifie que malgré le caractère aléatoire de chaque étape, le processus a généralement tendance à baisser. S'il avait une dérive positive, il augmenterait en moyenne. En revanche, le mouvement brownien standard n'a pas de tendance moyenne dans les deux sens. C'est ce qu'on appelle le mouvement brownien arithmétique car le terme de dérive s'échelonne uniquement avec l'incrément de temps, mais pas la valeur actuelle. Ainsi, cela affecte le processus de manière additive. Sigma est le terme de diffusion et adapte la volatilité. Le mouvement brownien géométrique est la solution au SDE

lequel est

Contrairement à l'ABM, le GBM est un processus multiplicatif ; alors que le terme de dérive en ABM est constant et s'ajoute à la valeur courante à chaque pas de temps, en GBM il est linéaire et est multiplié par la valeur courante. Le BM standard commence toujours à partir de 0 mais ABM et GBM n'ont pas à le faire.

La pertinence du mouvement brownien est qu'il est utile dans la modélisation des temps de mort / défaillance car le moment de la mort peut être représenté comme le temps d'arrêt du mouvement brownien. Le temps d'arrêt du mouvement brownien est défini comme la première fois que le processus atteint une valeur seuil B :

Le seuil B est appelé barrière absorbante. Les BM et ABM standard avec barrières absorbantes sont visualisés sur les Figure 1 et Figure 2 :

Figure 1. Mouvement brownien standard avec une barrière absorbante (la ligne rouge). 100 chemins d'échantillons simulés pour 1000 points dans le temps.
Figure 2. Mouvement brownien arithmétique avec une barrière absorbante (la ligne rouge). 100 chemins d'échantillons simulés pour 1000 points dans le temps. La dérive étant négative, nous approchons de la barrière par le haut.

Les distributions de temps d'arrêt des BM et ABM standards à barrières absorbantes constantes ont des solutions bien connues. Le temps d'arrêt du BM standard a une distribution Levy. Pour la dérivation, consultez le matériel de Kyle Siegrist ici . La preuve nécessite une compréhension du principe de réflexion, qui est clairement expliqué dans cette vidéo . Le temps d'arrêt d'ABM a une distribution gaussienne inverse (IG). Plusieurs preuves sont données dans ce post Stack Exchange . GBM peut être transformé en ABM comme nous le verrons ci-dessous.

La distribution Levy a le PDF :

où mu est le paramètre d'emplacement et c est le paramètre d'échelle. Le rapport entre la densité et le niveau de la barrière absorbante est c= B². À la queue, la densité décroît selon une loi de puissance, ce qui signifie que la distribution de Levy est une distribution à queue grasse. La figure 3 montre la densité et son évolution pour différentes valeurs du paramètre d'échelle :

Figure 3. La densité de la distribution de Levy pour différents paramètres d'échelle.

Le CDF de Levy est :

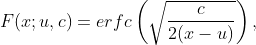
qui n'a pas de forme fermée. Ainsi, la fonction de risque devient

Lorsque nous traçons cette fonction pour des valeurs croissantes de x (qui dénote le temps puisque nous parlons de la distribution des durées de vie), nous obtenons un U inverse (Figure 4) :

Figure 4. La fonction de risque de la distribution de Levy augmente jusqu'à atteindre un pic, puis diminue asymptotiquement.

C'est aussi ce que Taleb a trouvé . Exemple de code Mathematica pour Levy avec emplacement = 0, échelle = 1 :

hf3[\[Sigma]_, x_] = HazardFunction[LevyDistribution[\[Mu] = 0, \[Sigma]], x] 
Plot[Table[hf3[\[Sigma], x], {\[Sigma], {1}}] // Évaluer, {x, 0, 3}]

Nous avons donc une période « pré-Lindy » comme l'appelle Taleb. Nous avons noté que le comportement asymptotique de la densité est une loi de puissance qui est approximativement :

que nous pouvons intégrer pour atteindre la fonction de survie sous une forme fermée

et obtenir la fonction de risque :

c'est ce que Taleb a obtenu par un itinéraire plus court. Il s'agit d'une fonction décroissante de façon monotone, qui correspond à ce que montre la figure 4 : un Lindy puissant intervient après un certain temps.

Ce que je ne comprends pas, c'est l'affirmation de Taleb selon laquelle « toute quantité de dérive négative fait que la distribution du temps d'arrêt sort de la classe de loi de puissance, perdant ainsi l'attribut « Lindy » » ( Remarque 8 à la p. 54 ). Certes, la dérive fait que la distribution du temps d'arrêt sort de la classe de loi de puissance, mais nous ne perdons pas vraiment l'attribut Lindy car la fonction de risque est qualitativement la même - un U inversé . Nous n'avions donc pas de Lindy fort en premier lieu et de Lindy faible dans les deux cas. Pourquoi donc? Comme mentionné, le mouvement brownien dérivé a une distribution IG, caractérisée par une moyenne et un paramètre de forme. Plus précisément, la distribution des temps d'arrêt des ABM avec dérive négative (Primozic, 2011) et une barrière absorbante B < S(0) est :

où mu est la dérive et sigma au carré est le terme de diffusion au carré. Dans le cas de GBM, si f Y(t) est un GBM, alors X(t)= log Y(t) est un ABM. Ainsi, la distribution du temps d'arrêt GBM avec la barrière absorbante L < S(0) est à nouveau IG, mais des paramètres transformés en log (Primozic, 2011 ; voir la solution du SDE pour le nouveau terme de dérive).

Le PDF de l'IG est

et le CDF est

Cela n'a pas de forme fermée, nous allons donc tracer la fonction de risque à partir de la formule h(x) = f(x)/(1-F(x)). La figure 5 montre la densité et la figure 6 montre la fonction de risque de la distribution IG pour différentes valeurs de moyenne et de forme.

Figure 5. La densité de la distribution gaussienne inverse.
Figure 6. La fonction de risque de la distribution gaussienne inverse.

Comme nous pouvons le voir sur la figure 6, le moment auquel Lindy entre en jeu dépend de la moyenne et de la forme de la distribution, qui à son tour dépendent de la dérive et de la distance entre la valeur de départ et la barrière absorbante. Mais qualitativement, tant le BM dérivé que le BM standard montrent un Lindy faible. Nous examinons maintenant quelques autres distributions qui peuvent être pertinentes pour l'effet Lindy.

4. Lois Lindy sans pouvoir

Nous pourrions dériver la survie puis la fonction de risque de la distribution de Weibull en intégrant son PDF, mais il existe une manière plus informative. La distribution de Weibull est en fait dérivée d'une fonction de risque spécifique ( Hogg, Tanis, & Zimmerman, 2013 ). Nous allons donc dériver son PDF de cette fonction de risque, plutôt que l'inverse. Nous verrons également que la fonction de risque décroît de façon monotone pour certaines valeurs de paramètres. Définir la fonction de risque cumulé :

Nous différencions pour obtenir la fonction de risque :

En rappelant les identités notées ci-dessus, la fonction de survie est

Puisque h(x) = f(x)/S(x), f(x) = h(x)S(x) . Alors, on obtient

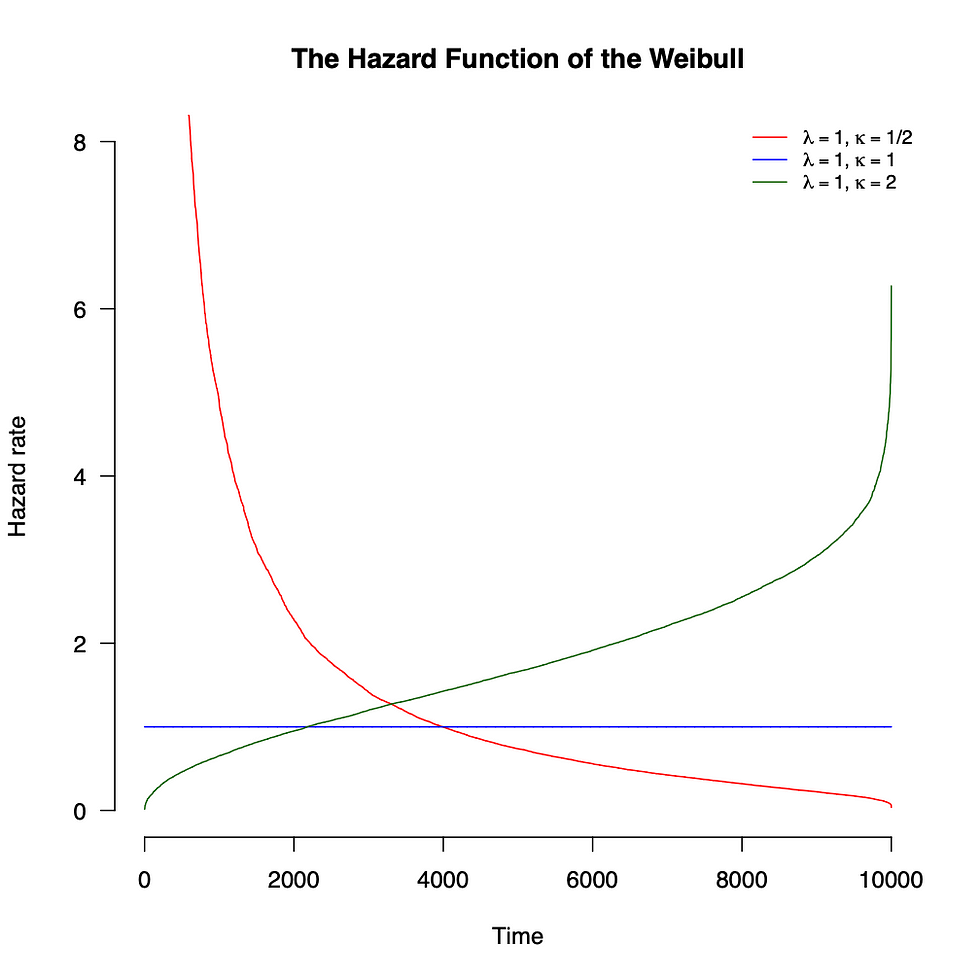
qui est la densité de la distribution de Weibull avec le paramètre de forme kappa et le paramètre d'échelle lambda. La densité est visualisée sur la figure 7 et la fonction de risque est visualisée sur la figure 8 pour différentes valeurs de forme. Notez que nous avons un Lindy fort avec une forme < 1. Pour une forme = 1, Weibull est réduit à la distribution exponentielle, qui est sans mémoire et a donc un risque constant.

Figure 7. La densité de la distribution de Weibull pour différentes valeurs de paramètres.
Figure 8. La fonction de risque de la distribution de Weibull pour différentes valeurs de forme. Pour la forme < 1, nous avons un Lindy fort.

La distribution Gamma est également flexible en ce qu'elle permet la modélisation de diverses fonctions de risque, mais elle n'est pas aussi répandue dans la littérature sur la fiabilité que la distribution de Weibull. Comme Weibull, Gamma peut donner un Lindy fort pour certaines valeurs de paramètres. La distribution Gamma modélise le temps d'attente jusqu'à ce qu'un nombre donné d'événements se produisent, et k représente le nombre d'événements. Il a également un paramètre d'échelle lambda, qui est le taux d'événements. Gamma a une fonction de risque décroissante lorsque k < 1. Mais comment peut-on avoir moins d'un événement ? Lorsque k < 1 - ou pas un entier en général - cela peut être interprété comme la capacité du système à résister aux chocs, ce qui est logique si l'on considère que pour les entiers, c'est le nombre d'événements de choc qui se produisent avant que le système ne tombe en panne. La distribution Gamma peut être dérivée de sa fonction de survie, mais l'expression simple de la fonction de survie ne fonctionne pas avec k < 1, nous devrons donc intégrer le PDF en utilisant ce qu'on appelle la fonction Gamma incomplète supérieure . Je voulais juste mentionner la belle affaire parce que si vous êtes intéressé, il y a une excellente explication par Aerin Kim . Je recommande également de lire la série qu'elle a écrite sur le Poisson et l' Exponentielle, qui sont nécessaires pour comprendre la distribution Gamma.

Le PDF gamma est

où

est la fonction Gamma. La densité est indiquée sur la figure 9.

Figure 9. La distribution gamma pour différentes valeurs de paramètres.

Pour obtenir la fonction de survie nous intégrons le PDF :

Pour éviter toute confusion, x est la variable temporelle et t n'est qu'une variable fictive. On retire les constantes :

Nous apportons la fonction à l'intérieur de l'intégrale à la forme familière de la fonction Gamma ci-dessus en modifiant les variables. Laisser

On réécrit le résultat avec les nouvelles variables et en changeant la borne inférieure d'intégration :

où Gamma(k, lambda*x) est la fonction Gamma incomplète supérieure. On obtient le hasard à partir de la formule habituelle :

qui décroît de façon monotone pour k < 1 (Figure 10).

Figure 10. La fonction de risque de la distribution Gamma pour différentes valeurs du paramètre de forme. Pour k < 1, cela donne Lindy fort.

5. Intuition pour l'effet des queues : ajout d'une barrière réfléchissante

Figure 11. La distribution de fréquence des temps d'arrêt du GBM lorsqu'il est délimité par une barrière réfléchissante.

Ensuite, j'ai utilisé le package « bshazard » (Rebore, Salim et Reilly, 2018) pour obtenir une estimation non paramétrique des taux de risque (Figure 12). Comme nous pouvons le voir, les taux de risque fluctuent autour d'un niveau constant pendant un certain temps, puis augmentent à un point où pratiquement tous les chemins d'échantillonnage sont morts. Donc pas de Lindy.

Figure 12. La fonction de risque estimée des temps d'arrêt du GBM lorsqu'elle est délimitée par une barrière réfléchissante.

6. Conclusion

Plus de Eren Asena

Étudiant diplômé en psychologie, sciences informatiques

Labels: ,