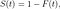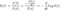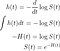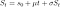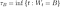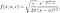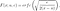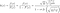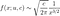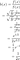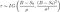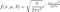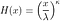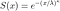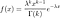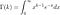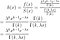L'effet Lindy

L'effet Lindy : le concept et les mathématiques

Nassim N. Taleb a récemment publié son officialisation de l'effet Lindy . J'ai écrit cet article pour développer ses idées. J'ai utilisé R pour tout tracer et vous pouvez trouver le code ici , mais je fournis également un exemple de code Mathematica.

Eren Asena

(automatic translation)

Un aperçu de ce que je veux discuter:

1. Une introduction conceptuelle à l'effet Lindy
2. L'effet Lindy comme fonction de risque décroissante
3. Mouvement brownien : Lindy fort contre faible
4. Lindy a-t-il besoin de lois de puissance ? Les distributions de Weibull et Gamma
5. Intuition pour l' effet de queues : Tuer Lindy avec une barrière réfléchissante
6. Conclusion

1. Introduction

L'effet Lindy est l'idée que l'espérance de vie restante d'une augmentation de chose non périssables wje e âge - le plus il est élevé , plus il est probable de survivre. Non périssable signifie que la chose que nous considérons n'a pas de limite organique à sa durée de vie (par exemple, les technologies, les idées, etc.). Ainsi, la musique de Beethoven a plus de chances de survivre que celle de Taylor Swift, et la Bible a plus de chances de survivre que Harry Potter. L'idée a été explorée pour la première fois par Benoit Mandelbrot dans The Fractal Geometry of Nature (1982) et popularisée par Nassim N. Taleb dans son livre de 2012 Antifragile . Taleb a fourni un cadre pour réfléchir à l'effet Lindy, expliquant qu'il implique l' antifragilitéÀ travers le temps. Alors que les choses fragiles sont affectées par le stress / la volatilité, les choses antifragiles en profitent. Le temps étant un facteur de stress, les choses qui montrent l'effet Lindy profitent du temps. Taleb a écrit que sans borne supérieure naturelle, la distribution d'un temps d'événement « … n'est contrainte que par la fragilité » et suit une loi de puissance ( Antifragile , p. 317 de la publication 2014). Dans ces circonstances, l'espérance de vie restante est proportionnelle à la survie passée. Par exemple, l'espérance de vie d'une technologie vieille de 100 ans devrait être dix fois plus longue que l'espérance de vie d'une technologie vieille de 10 ans. Cependant, l'espérance de vie est une « moyenne dérivée de manière probabiliste » ( Antifragile, p. 319), ce qui signifie que nous ne parlons pas d'une loi naturelle.

Pendant de nombreuses années, l'effet Lindy n'a pas eu de formalisation mathématique établie. Le statisticien John D. Cook a souligné en 2012 que Lindy signifiait une fonction de risque décroissante. Cet article a analysé la distribution de Pareto en utilisant la même logique, montrant qu'elle implique l'effet Lindy. J'expliquerai la signification d'une fonction de risque et comment en calculer une ci-dessous. Mais l'idée d'utiliser des fonctions de hasard pour formaliser l'effet Lindy n'a germé que récemment . Il y a quelques années, Taleb a commencé à utiliser le temps d'arrêt du mouvement brownienpour explorer l'effet Lindy. Dans son travail récent que j'ai lié ci-dessus, il a analysé la distribution du temps d'arrêt à l'aide de fonctions de survie et de risque. Il est important de comprendre ce qu'il a fait là-bas. Donc, je vais d'abord décrire les fonctions qui définissent l'effet Lindy. Ensuite, je donnerai un aperçu de ce qu'est le mouvement brownien et pourquoi il est logique de l'utiliser lors de l'étude de Lindy. Après avoir examiné le comportement de Lindy avec le mouvement brownien, nous analyserons quelques distributions de probabilité et verrons que dans certaines conditions, des durées de vie à queue lourde qui ne suivent pas une loi de puissance peuvent toujours montrer l'effet Lindy.

2. L'effet Lindy comme fonction de danger décroissant

Après avoir défini conceptuellement l'effet Lindy, définissons-le mathématiquement. Une chose obéit à l'effet Lindy si l'espérance conditionnelle de sa durée de vie restante au-delà d'un point dans le temps, étant donné qu'elle a survécu jusqu'à ce point, augmente (Eliazar, 2017). Que ce soit ou non le cas peut être testé avec une analyse de survie ( Aalen & Gjessing, 2001 ). L'analyse de survie examine le temps entre un point de départ et un événement tel que la mort. L'objectif est d'analyser la distribution de probabilité de ce temps, en utilisant des fonctions de survie et de risque. Si la probabilité conditionnelle de survie augmente, alors la probabilité conditionnelle de mourir dans un intervalle de temps, compte tenu de la survie jusque-là, devrait diminuer. Si nous divisons cette probabilité par la longueur de l'intervalle de temps que nous considérons, nous obtenons lefonction de risque , également appelée « force de mortalité », ou taux instantané de décès/d'échec. Écrire ceci officiellement clarifiera, espérons-le, ce que je viens de dire. Si X est l'heure du décès, on s'intéresse à :

Notez que puisqu'il s'agit d'un taux et non d'une probabilité, il peut prendre des valeurs supérieures à 1. Le taux de risque peut être calculé à l'aide de l'expression suivante :

où f(t) est la fonction de densité et S(t) est la fonction de survie. La fonction de survie d'une distribution évaluée à une valeur donne la probabilité que la variable aléatoire soit plus grande que cette valeur, P(T > t). La fonction de survie est donnée par

où F(t) est la fonction de distribution cumulative (CDF). Le CDF donne la probabilité que la durée de vie prenne une valeur inférieure ou égale à un instant donné, donc la fonction de survie est le complément du CDF. L'intégration de la fonction de risque donne la fonction de risque cumulé H(t), qui est le risque de décès cumulé jusqu'à un instant donné t . Notez les identités suivantes qui seront utiles lorsque nous dérivons des fonctions de risque :

La fonction de densité est la dérivée de la CDF, qui est le complément de la fonction de survie, donc lorsque nous différencions la fonction de survie et changeons de signe, nous récupérons la fonction de densité. La dernière identité découle de la différenciation d'un logarithme. Maintenant, nous écrivons la fonction de survie en termes de risque cumulé :

En résumé, la fonction de risque donne le taux de mortalité immédiatement après un point, compte tenu de la survie jusqu'à ce point. Une fonction de risque décroissante signifie que les chances de survie s'améliorent avec le temps - l'effet Lindy. Souvent, une fonction de risque n'est pas monotone mais a une forme en U inversé ; il augmente jusqu'à atteindre une valeur maximale, puis diminue asymptotiquement. Cela signifie que Lindy a besoin de temps pour entrer en action. Taleb a appelé une fonction de risque décroissante de manière monotone « la forte propriété de Pareto ». Par souci de simplicité, appelons-le « Lindy fort » lorsque nous avons une fonction de risque entièrement non croissante et « Lindy faible » lorsqu'elle augmente d'abord puis diminue. Nous allons maintenant examiner quelques exemples de fonctions de risque, en commençant par le temps d'arrêt du mouvement brownien.

3. Mouvement brownien et effet Lindy

Le mouvement brownien (BM) est le mouvement stochastique des particules dans le fluide. Il a été découvert par le botaniste Robert Brown en observant le comportement des grains de pollen dans l'eau. Il a décrit ce comportement comme irrégulier et apparemment aléatoire. Plus tard, Einstein a montré que le comportement de ces particules était en effet aléatoire et indépendant du mouvement passé. Bien que la signification originale du mouvement brownien ait été de prouver l'existence d'atomes et de molécules, les fluctuations aléatoires qu'il décrit peuvent être observées dans de nombreux phénomènes. Par exemple, le mouvement brownien est utilisé en finance pour modéliser les cours des actions. Le mouvement brownien a trois formes principales : le mouvement brownien standard, le mouvement brownien arithmétique (c'est-à-dire le BM dérivé) (ABM) et le mouvement brownien géométrique (GBM). Je vais décrire brièvement chacun.

Un processus stochastique à valeur réelle W(t) est un mouvement brownien standard (également appelé processus de Wiener) s'il possède les propriétés suivantes (Dahl, 2010) :

1. Le processus commence à W(0) = 0.
2. Le processus a des incréments indépendants : pour tout t > 0, l'incrément W(t+s)–W(t) est une variable aléatoire indépendante.
3. Les incréments sont normaux : W(t+s)–W(t)~N(0, s).
4. Le processus est continu dans le temps.

Un processus stochastique S(t) est un mouvement brownien arithmétique s'il suit l'équation différentielle stochastique (SDE) :

avec la valeur initiale S(0) = s(0). Cela a la solution

où mu est le terme de dérive et sera négatif dans notre cas. Avoir une dérive négative signifie que malgré le caractère aléatoire de chaque étape, le processus a généralement tendance à baisser. S'il avait une dérive positive, il augmenterait en moyenne. En revanche, le mouvement brownien standard n'a pas de tendance moyenne dans les deux sens. C'est ce qu'on appelle le mouvement brownien arithmétique car le terme de dérive s'échelonne uniquement avec l'incrément de temps, mais pas la valeur actuelle. Ainsi, cela affecte le processus de manière additive. Sigma est le terme de diffusion et adapte la volatilité. Le mouvement brownien géométrique est la solution au SDE

lequel est

Contrairement à l'ABM, le GBM est un processus multiplicatif ; alors que le terme de dérive en ABM est constant et s'ajoute à la valeur courante à chaque pas de temps, en GBM il est linéaire et est multiplié par la valeur courante. Le BM standard commence toujours à partir de 0 mais ABM et GBM n'ont pas à le faire.

La pertinence du mouvement brownien est qu'il est utile dans la modélisation des temps de mort / défaillance car le moment de la mort peut être représenté comme le temps d'arrêt du mouvement brownien. Le temps d'arrêt du mouvement brownien est défini comme la première fois que le processus atteint une valeur seuil B :

Le seuil B est appelé barrière absorbante. Les BM et ABM standard avec barrières absorbantes sont visualisés sur les Figure 1 et Figure 2 :

Figure 1. Mouvement brownien standard avec une barrière absorbante (la ligne rouge). 100 chemins d'échantillons simulés pour 1000 points dans le temps.

Figure 2. Mouvement brownien arithmétique avec une barrière absorbante (la ligne rouge). 100 chemins d'échantillons simulés pour 1000 points dans le temps. La dérive étant négative, nous approchons de la barrière par le haut.

Les distributions de temps d'arrêt des BM et ABM standards à barrières absorbantes constantes ont des solutions bien connues. Le temps d'arrêt du BM standard a une distribution Levy. Pour la dérivation, consultez le matériel de Kyle Siegrist ici . La preuve nécessite une compréhension du principe de réflexion, qui est clairement expliqué dans cette vidéo . Le temps d'arrêt d'ABM a une distribution gaussienne inverse (IG). Plusieurs preuves sont données dans ce post Stack Exchange . GBM peut être transformé en ABM comme nous le verrons ci-dessous.

La distribution Levy a le PDF :

où mu est le paramètre d'emplacement et c est le paramètre d'échelle. Le rapport entre la densité et le niveau de la barrière absorbante est c= B². À la queue, la densité décroît selon une loi de puissance, ce qui signifie que la distribution de Levy est une distribution à queue grasse. La figure 3 montre la densité et son évolution pour différentes valeurs du paramètre d'échelle :

Figure 3. La densité de la distribution de Levy pour différents paramètres d'échelle.

Le CDF de Levy est :

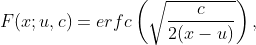
qui n'a pas de forme fermée. Ainsi, la fonction de risque devient

Lorsque nous traçons cette fonction pour des valeurs croissantes de x (qui dénote le temps puisque nous parlons de la distribution des durées de vie), nous obtenons un U inverse (Figure 4) :

Figure 4. La fonction de risque de la distribution de Levy augmente jusqu'à atteindre un pic, puis diminue asymptotiquement.

C'est aussi ce que Taleb a trouvé . Exemple de code Mathematica pour Levy avec emplacement = 0, échelle = 1 :

hf3[\[Sigma]_, x_] = HazardFunction[LevyDistribution[\[Mu] = 0, \[Sigma]], x] 
Plot[Table[hf3[\[Sigma], x], {\[Sigma], {1}}] // Évaluer, {x, 0, 3}]

Nous avons donc une période « pré-Lindy » comme l'appelle Taleb. Nous avons noté que le comportement asymptotique de la densité est une loi de puissance qui est approximativement :

que nous pouvons intégrer pour atteindre la fonction de survie sous une forme fermée

et obtenir la fonction de risque :

c'est ce que Taleb a obtenu par un itinéraire plus court. Il s'agit d'une fonction décroissante de façon monotone, qui correspond à ce que montre la figure 4 : un Lindy puissant intervient après un certain temps.

Ce que je ne comprends pas, c'est l'affirmation de Taleb selon laquelle « toute quantité de dérive négative fait que la distribution du temps d'arrêt sort de la classe de loi de puissance, perdant ainsi l'attribut « Lindy » » ( Remarque 8 à la p. 54 ). Certes, la dérive fait que la distribution du temps d'arrêt sort de la classe de loi de puissance, mais nous ne perdons pas vraiment l'attribut Lindy car la fonction de risque est qualitativement la même - un U inversé . Nous n'avions donc pas de Lindy fort en premier lieu et de Lindy faible dans les deux cas. Pourquoi donc? Comme mentionné, le mouvement brownien dérivé a une distribution IG, caractérisée par une moyenne et un paramètre de forme. Plus précisément, la distribution des temps d'arrêt des ABM avec dérive négative (Primozic, 2011) et une barrière absorbante B < S(0) est :

où mu est la dérive et sigma au carré est le terme de diffusion au carré. Dans le cas de GBM, si f Y(t) est un GBM, alors X(t)= log Y(t) est un ABM. Ainsi, la distribution du temps d'arrêt GBM avec la barrière absorbante L < S(0) est à nouveau IG, mais des paramètres transformés en log (Primozic, 2011 ; voir la solution du SDE pour le nouveau terme de dérive).

Le PDF de l'IG est

et le CDF est

Cela n'a pas de forme fermée, nous allons donc tracer la fonction de risque à partir de la formule h(x) = f(x)/(1-F(x)). La figure 5 montre la densité et la figure 6 montre la fonction de risque de la distribution IG pour différentes valeurs de moyenne et de forme.

Figure 5. La densité de la distribution gaussienne inverse.

Figure 6. La fonction de risque de la distribution gaussienne inverse.

Comme nous pouvons le voir sur la figure 6, le moment auquel Lindy entre en jeu dépend de la moyenne et de la forme de la distribution, qui à son tour dépendent de la dérive et de la distance entre la valeur de départ et la barrière absorbante. Mais qualitativement, tant le BM dérivé que le BM standard montrent un Lindy faible. Nous examinons maintenant quelques autres distributions qui peuvent être pertinentes pour l'effet Lindy.

4. Lois Lindy sans pouvoir

La distribution de Weibull est populaire dans les domaines qui utilisent l'analyse de survie, tels que la science actuarielle et l'ingénierie. La raison en est qu'il peut modéliser toutes sortes de fonctions de risque, qu'elles soient croissantes, décroissantes ou constantes. Tout dépend de la valeur de son paramètre de forme, comme nous le verrons dans une seconde. La distribution de Weibull peut également avoir des queues lourdes et être utile dans la modélisation d'observations extrêmes. Mais ses queues ne sont pas aussi lourdes que celles d'une distribution de loi de puissance, ce qui signifie que les valeurs extrêmes ne sont pas aussi probables sous un modèle de Weibull qu'elles le sont sous un modèle de loi de puissance ( Kizilersu, Kreer, & Thomas, 2018 ).

Nous pourrions dériver la survie puis la fonction de risque de la distribution de Weibull en intégrant son PDF, mais il existe une manière plus informative. La distribution de Weibull est en fait dérivée d'une fonction de risque spécifique ( Hogg, Tanis, & Zimmerman, 2013 ). Nous allons donc dériver son PDF de cette fonction de risque, plutôt que l'inverse. Nous verrons également que la fonction de risque décroît de façon monotone pour certaines valeurs de paramètres. Définir la fonction de risque cumulé :

Nous différencions pour obtenir la fonction de risque :

En rappelant les identités notées ci-dessus, la fonction de survie est

Puisque h(x) = f(x)/S(x), f(x) = h(x)S(x) . Alors, on obtient

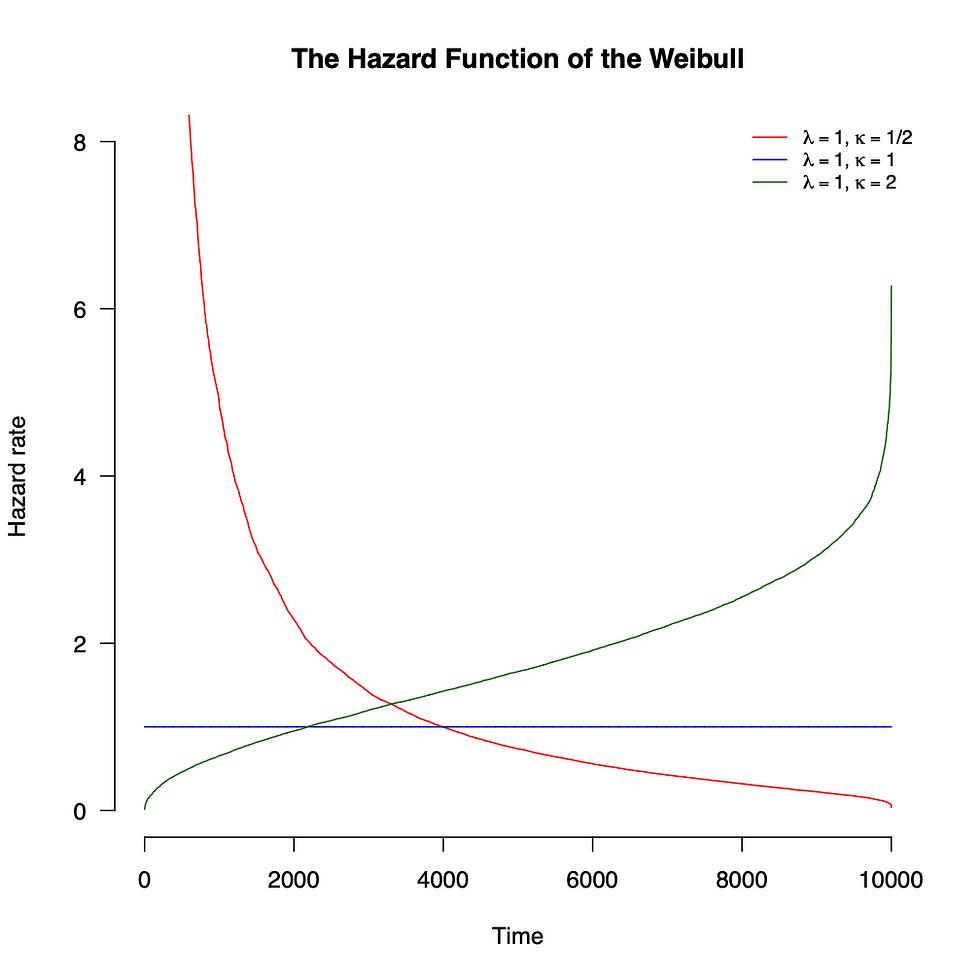
qui est la densité de la distribution de Weibull avec le paramètre de forme kappa et le paramètre d'échelle lambda. La densité est visualisée sur la figure 7 et la fonction de risque est visualisée sur la figure 8 pour différentes valeurs de forme. Notez que nous avons un Lindy fort avec une forme < 1. Pour une forme = 1, Weibull est réduit à la distribution exponentielle, qui est sans mémoire et a donc un risque constant.

Figure 7. La densité de la distribution de Weibull pour différentes valeurs de paramètres.

Figure 8. La fonction de risque de la distribution de Weibull pour différentes valeurs de forme. Pour la forme < 1, nous avons un Lindy fort.

La distribution Gamma est également flexible en ce qu'elle permet la modélisation de diverses fonctions de risque, mais elle n'est pas aussi répandue dans la littérature sur la fiabilité que la distribution de Weibull. Comme Weibull, Gamma peut donner un Lindy fort pour certaines valeurs de paramètres. La distribution Gamma modélise le temps d'attente jusqu'à ce qu'un nombre donné d'événements se produisent, et k représente le nombre d'événements. Il a également un paramètre d'échelle lambda, qui est le taux d'événements. Gamma a une fonction de risque décroissante lorsque k < 1. Mais comment peut-on avoir moins d'un événement ? Lorsque k < 1 - ou pas un entier en général - cela peut être interprété comme la capacité du système à résister aux chocs, ce qui est logique si l'on considère que pour les entiers, c'est le nombre d'événements de choc qui se produisent avant que le système ne tombe en panne. La distribution Gamma peut être dérivée de sa fonction de survie, mais l'expression simple de la fonction de survie ne fonctionne pas avec k < 1, nous devrons donc intégrer le PDF en utilisant ce qu'on appelle la fonction Gamma incomplète supérieure . Je voulais juste mentionner la belle affaire parce que si vous êtes intéressé, il y a une excellente explication par Aerin Kim . Je recommande également de lire la série qu'elle a écrite sur le Poisson et l' Exponentielle, qui sont nécessaires pour comprendre la distribution Gamma.

Le PDF gamma est

où

est la fonction Gamma. La densité est indiquée sur la figure 9.

Figure 9. La distribution gamma pour différentes valeurs de paramètres.

Pour obtenir la fonction de survie nous intégrons le PDF :

Pour éviter toute confusion, x est la variable temporelle et t n'est qu'une variable fictive. On retire les constantes :

Nous apportons la fonction à l'intérieur de l'intégrale à la forme familière de la fonction Gamma ci-dessus en modifiant les variables. Laisser

On réécrit le résultat avec les nouvelles variables et en changeant la borne inférieure d'intégration :

où Gamma(k, lambda*x) est la fonction Gamma incomplète supérieure. On obtient le hasard à partir de la formule habituelle :

qui décroît de façon monotone pour k < 1 (Figure 10).

Figure 10. La fonction de risque de la distribution Gamma pour différentes valeurs du paramètre de forme. Pour k < 1, cela donne Lindy fort.

5. Intuition pour l'effet des queues : ajout d'une barrière réfléchissante

Bien que l'effet Lindy ne nécessite pas de loi de puissance, il a besoin de queues lourdes. Revenons un instant au mouvement brownien. Que se passe-t-il si nous ajoutons une barrière réfléchissante au-dessus ? La barrière réfléchissante ne tue pas le processus mais garde simplement sa valeur la même jusqu'à ce qu'elle descende, limitant ainsi les durées de vie d'en haut. Cela coupe la queue, mettant vraisemblablement la distribution dans la classe exponentielle. Je n'ai pas pu trouver la densité du temps d'arrêt, alors je l'ai simulé avec GBM et j'ai créé un histogramme (Figure 11). La distribution du temps d'arrêt d'un GBM avec une barrière absorbante en dessous et une barrière réfléchissante au-dessus a une queue beaucoup plus légère :

Figure 11. La distribution de fréquence des temps d'arrêt du GBM lorsqu'il est délimité par une barrière réfléchissante.

Ensuite, j'ai utilisé le package « bshazard » (Rebore, Salim et Reilly, 2018) pour obtenir une estimation non paramétrique des taux de risque (Figure 12). Comme nous pouvons le voir, les taux de risque fluctuent autour d'un niveau constant pendant un certain temps, puis augmentent à un point où pratiquement tous les chemins d'échantillonnage sont morts. Donc pas de Lindy.

Figure 12. La fonction de risque estimée des temps d'arrêt du GBM lorsqu'elle est délimitée par une barrière réfléchissante.

6. Conclusion

Résumons. Nous avons d'abord examiné la définition de l'effet Lindy, qui signifie que l'espérance de vie restante augmente en fonction de l'âge. Taleb et d'autres ont souligné que les distributions de loi de puissance comme Pareto ont cette propriété. Ce concept est mathématiquement capturé par une fonction de risque décroissante, ce qui signifie que le taux de décès conditionnel diminue avec le temps. Le mouvement brownien avec une barrière absorbante apparaît comme un choix naturel pour modéliser ce phénomène, car il s'agit d'un processus stochastique avec une fin définie, tout comme la vie. L'analyse du temps d'arrêt du mouvement brownien donne deux distributions : Levy et la gaussienne inverse. La première est une distribution à queue épaisse avec un comportement en loi de puissance asymptotique, la seconde ne l'est pas. Les deux ont un taux de risque en forme de U inversé, ce qui signifie que Lindy met un certain temps à entrer en action. Nous avons appelé cela Lindy faible. Strong Lindy est une fonction de risque non croissante. Nous avons ensuite montré que les distributions à queue lourde qui ne suivent pas une loi de puissance, telles que les distributions de Weibull et Gamma pour certaines valeurs de paramètres, peuvent également donner un Lindy fort. Enfin, nous avons ajouté une barrière réfléchissante à BM, montrant que la limitation des durées de vie par le dessus tue l'effet Lindy. Il n'y a rien de nouveau là-dedans - cela donne juste une bonne intuition.

Plus de Eren Asena

Étudiant diplômé en psychologie, sciences informatiques

behind the muses

 

The stories behind the muses

We often share stories of artists in relation to what inspires them. When that inspiration comes from individuals, those individuals' stories deserve to be told as well. From women painting women to neglected Black sitters and from revisiting the bohemian muse to the Tahitian woman behind Paul Gauguin's paintings, these stories help us to reconsider the trope of the muse.

Fanny Eaton: Jamaican Pre-Raphaelite muse Isabel Rawsthorne: artist and muse The naked muse: to see or be seen? More than muses: the women at the centre of Surrealism The art of Celia Paul: a mistaken muse The queer love story behind Virginia Woolf's 'Orlando' Recapturing the gaze: female artists and portraiture

Above Mother, c.1976–1981, oil on hardboard by Celia Paul (b.1959). © the artist. Photo credit: UCL Culture ART UK

côté obscur d'Internet

 

Il a prédit le côté obscur d'Internet il y a 30 ans.

 Pourquoi personne n'a écouté ?

En 1994 — avant que la plupart des Américains n'aient une adresse e-mail ou un accès Internet ou même un ordinateur personnel — Philip Agre prévoyait que les ordinateurs faciliteraient un jour la collecte massive de données sur tout dans la société. Puis il a disparu, laissant derrière lui un héritage de travail qui était étrangement prémonitoire dans la prédiction de l'impact de la technologie sur la société.

Par Reed Albergotti 

(automatic translation) 

En 1994 — avant que la plupart des Américains n'aient une adresse e-mail ou un accès Internet ou même un ordinateur personnel — Philip Agre prévoyait que les ordinateurs faciliteraient un jour la collecte massive de données sur tout dans la société.

Ce processus changerait et simplifierait le comportement humain, écrivait le professeur de sciences humaines de l'époque à l'UCLA. Et parce que ces données ne seraient pas collectées par un seul et puissant gouvernement « grand frère », mais par de nombreuses entités à des fins différentes, il a prédit que les gens se sépareraient volontairement de quantités massives d'informations sur leurs peurs et leurs désirs les plus personnels.

"Des développements vraiment inquiétants peuvent sembler" pas si mauvais " simplement parce qu'ils manquent des horreurs manifestes de la dystopie d'Orwell ", a écrit Agre, qui a un doctorat en informatique du Massachusetts Institute of Technology, dans un article universitaire.

Près de 30 ans plus tard, l'article d'Agre semble étrangement prémonitoire, une vision surprenante d'un avenir qui s'est réalisé sous la forme d'un complexe industriel de données qui ne connaît pas de frontières et peu de lois. Les données collectées par des réseaux publicitaires et des applications mobiles disparates à de multiples fins sont utilisées pour influencer les élections ou, dans au moins un cas, pour dénoncer un prêtre gay . Mais Agre ne s'est pas arrêté là. Il a prévu l'utilisation abusive autoritaire de la technologie de reconnaissance faciale, il a prédit notre incapacité à résister à une désinformation bien conçue et il a prédit que l'intelligence artificielle serait utilisée à des fins obscures si elle n'était pas soumise à une enquête morale et philosophique.

Ensuite, personne n'a écouté. Aujourd'hui, de nombreux anciens collègues et amis d'Agre disent qu'ils ont davantage pensé à lui ces dernières années et qu'ils ont relu son travail, alors que les pièges de la croissance explosive et incontrôlée d'Internet sont apparus, érodant la démocratie et contribuant à faciliter un soulèvement violent. sur les marches du Capitole des États-Unis en janvier.

Google a engagé Timnit Gebru pour critiquer ouvertement l'IA contraire à l'éthique. Puis elle a été licenciée pour ça.

"Nous vivons au lendemain de l'ignorance de gens comme Phil", a déclaré Marc Rotenberg, qui a édité un livre avec Agre en 1998 sur la technologie et la confidentialité, et est maintenant fondateur et directeur exécutif du Center for AI and Digital Policy.

Charlotte Lee, qui a étudié sous Agre en tant qu'étudiante diplômée à l'UCLA et est maintenant professeure de conception et d'ingénierie centrée sur l'humain à l'Université de Washington, a déclaré qu'elle étudiait toujours son travail et en apprenait aujourd'hui. Elle a dit qu'elle souhaitait qu'il soit là pour l'aider à mieux le comprendre.

Mais Agre n'est pas disponible. En 2009, il a tout simplement abandonné la surface de la terre, abandonnant son poste à l'UCLA. Lorsque des amis ont signalé la disparition d'Agre, la police l'a localisé et a confirmé qu'il allait bien, mais Agre n'est jamais revenu dans le débat public. Ses amis les plus proches ont refusé de discuter davantage des détails de sa disparition, invoquant le respect de la vie privée d'Agre.

Au lieu de cela, bon nombre des idées et des conclusions qu'Agre a explorées dans ses recherches universitaires et ses écrits n'apparaissent que récemment dans les groupes de réflexion et les organisations à but non lucratif axés sur la responsabilisation des entreprises technologiques.

"Je vois des choses sur lesquelles Phil a écrit dans les années 90 être dites aujourd'hui comme s'il s'agissait de nouvelles idées", a déclaré Christine Borgman, professeur d'informatique à l'UCLA qui a aidé à recruter Agre pour son poste de professeur à l'école.

Le Washington Post a envoyé un message à la dernière adresse e-mail connue d'Agre. Il a rebondi. Les tentatives pour contacter sa sœur et d'autres membres de la famille ont été infructueuses. Une dizaine d'anciens collègues et amis n'avaient aucune idée de l'endroit où Agre habite aujourd'hui. Certains ont dit qu'il y a quelques années, il vivait quelque part autour de Los Angeles.

Une étude fédérale confirme les préjugés raciaux de nombreux systèmes de reconnaissance faciale, jette un doute sur leur utilisation croissante

Agre était un enfant prodige des mathématiques qui est devenu un blogueur populaire et un contributeur à Wired. Maintenant, il a été presque oublié dans les cercles technologiques traditionnels. Mais son travail est encore régulièrement cité par les chercheurs en technologie dans le milieu universitaire et est considéré comme une lecture fondamentale dans le domaine de l'informatique sociale, ou l'étude des effets des ordinateurs sur la société.

Agre a obtenu son doctorat au MIT en 1989, la même année où le World Wide Web a été inventé. À cette époque, même parmi les investisseurs en capital-risque de la Silicon Valley pariant sur l'essor de l'informatique, peu de gens prévoyaient à quel point l'informatisation de tout allait changer profondément et rapidement la vie, l'économie ou même la politique.

Un petit groupe d'universitaires, Agre inclus, a observé que les informaticiens considéraient leur travail dans un vide largement déconnecté du monde qui les entourait. Dans le même temps, les gens en dehors de ce monde n'avaient pas une compréhension suffisamment profonde de la technologie ou de la façon dont elle était sur le point de changer leur vie.

Au début des années 1990, Agre en est venu à croire que le domaine de l'intelligence artificielle s'était égaré et que le manque de critique de la profession en était l'une des principales raisons. À ces débuts de l'intelligence artificielle, la plupart des spécialistes de l'IA se concentraient sur des problèmes mathématiques complexes visant à automatiser des tâches humaines, avec un succès limité. Pourtant, l'industrie a décrit le code qu'elle écrivait comme « intelligent », lui donnant des attributs humains qui n'existaient pas réellement.

Son point de repère 1997 papier appelé « leçons apprises en essayant de réforme AI » est encore largement considéré comme un classique, a déclaré Geoffrey Bowker, professeur émérite de l' informatique à l' Université de Californie à Irvine. Agre a remarqué que ceux qui construisaient l'intelligence artificielle ignoraient les critiques de la technologie de la part des étrangers. Mais Agre a fait valoir que la critique devrait faire partie du processus de construction de l'IA. « La conclusion est assez brillante et nous a pris en tant que domaine de nombreuses années à comprendre. Un pied planté dans l'artisanat du design et l'autre pied planté dans la critique », a déclaré Bowker.

Néanmoins, l'IA a progressé sans encombre, s'intégrant même dans des industries « low-tech » et affectant la vie de la plupart des personnes qui utilisent Internet. Il guide les gens sur ce qu'il faut regarder et lire sur YouTube et Facebook, il détermine les peines pour les criminels condamnés, permet aux entreprises d'automatiser et de supprimer des emplois, et permet aux régimes autoritaires de surveiller les citoyens avec une plus grande efficacité et de contrecarrer les tentatives de démocratie.

Le PDG de Google, Sundar Pichai : les craintes concernant l'intelligence artificielle sont "très légitimes", déclare-t-il dans une interview à Post

L'IA d'aujourd'hui, qui a largement abandonné le type de travail qu'Agre et d'autres faisaient dans les années 80 et 90, se concentre sur l'ingestion de quantités massives de données et leur analyse avec les ordinateurs les plus puissants du monde. Mais au fur et à mesure que la nouvelle forme d'IA a progressé, elle a créé des problèmes - allant de la discrimination aux bulles de filtrage à la propagation de la désinformation - et certains universitaires disent que c'est en partie parce qu'elle souffre du même manque d'autocritique qu'Agre a identifié 30 il y a des années.

En décembre, le limogeage par Google du chercheur en IA Timnit Gebru après avoir écrit un article sur les problèmes éthiques auxquels sont confrontés les efforts de Google en matière d'IA a mis en évidence la tension continue sur l'éthique de l'intelligence artificielle et l'aversion de l'industrie pour la critique.

"C'est un domaine tellement homogène, et les gens dans ce domaine ne voient pas que ce qu'ils font pourrait être critiqué", a déclaré Sofian Audry, professeur de médias informatiques à l'Université du Québec à Montréal qui a commencé comme chercheur en intelligence artificielle. . "Ce que dit Agre, c'est qu'il est utile et nécessaire que les personnes qui développent ces technologies soient critiques", a déclaré Audrey.

Agre a grandi dans le Maryland, où il a dit qu'il avait été "construit pour être un prodige des mathématiques" par un psychologue de la région. Il a déclaré dans son article de 1997 que l'intégration scolaire a conduit à une recherche d'étudiants doués et talentueux. Agre s'est ensuite mis en colère contre ses parents pour l'avoir envoyé à l'université trop tôt et sa relation avec eux en a souffert, selon un ami, qui a parlé sous couvert d'anonymat car Agre ne lui a pas donné la permission de parler de sa vie personnelle.

Agre a écrit que lorsqu'il est entré à l'université, il n'était pas obligé d'apprendre autre chose que les mathématiques et "est arrivé à l'école supérieure du MIT avec peu de connaissances réelles au-delà des mathématiques et des ordinateurs". Il a pris une année sabbatique pour voyager et lire, "en essayant de manière aveugle et avec mes propres ressources, de devenir une personne instruite", a-t-il écrit.

Agre a commencé à se rebeller, dans un sens, de sa profession, cherchant des critiques de l'intelligence artificielle, étudiant la philosophie et d'autres disciplines académiques. Au début, il trouvait les textes « impénétrables », écrivait-il, parce qu'il avait entraîné son esprit à disséquer tout ce qu'il lisait comme il le ferait avec un article technique sur les mathématiques ou l'informatique. « Il m'est finalement venu à l'esprit d'arrêter de traduire ces étranges langages disciplinaires en schémas techniques, et de simplement les apprendre selon leurs propres termes », écrit-il.

L'intérêt intellectuel grandissant d'Agre l'a éloigné de l'informatique et l'a transformé en quelque chose d'inhabituel à l'époque : un brillant mathématicien avec une compréhension approfondie des théories les plus avancées de l'intelligence artificielle, qui pouvait également sortir de ce domaine et le regarder de manière critique depuis le point de vue d'un étranger.

Un bulletin catholique promettait du journalisme d'investigation. Ensuite, il a sorti un prêtre en utilisant les données de Grindr.

Pour cette raison, Agre est devenu un universitaire recherché. Plusieurs anciens collègues ont raconté des histoires sur l'appétit insatiable d'Agre pour les livres du paysage académique et populaire, empilés dans son bureau ou dans la bibliothèque. Il est devenu connu pour sa pensée originale qui a été soutenue par sa curiosité généralisée.

"C'était une personne très instructive avec qui penser – quelqu'un avec qui vous voudriez prendre un repas à chaque occasion", a déclaré Borgman.

Agre a combiné sa compréhension des sciences humaines et de la technologie pour disséquer l'impact que la technologie aurait sur la société à mesure qu'elle progressait. Aujourd'hui, nombre de ses analyses se lisent comme des prédictions qui se réalisent.

Dans un article de 1994 , publié un an avant les lancements de Yahoo, Amazon et eBay, Agre prévoyait que les ordinateurs pourraient faciliter la collecte massive de données sur tout dans la société, et que les gens négligeraient les problèmes de confidentialité parce que, plutôt que "grand frère" collecter des données pour surveiller les citoyens, ce serait de nombreuses entités différentes qui collecteraient les données à de nombreuses fins, certaines bonnes et d'autres problématiques.

Plus profondément, cependant, Agre a écrit dans le document que la collecte de masse de données changerait et simplifierait le comportement humain pour le rendre plus facile à quantifier. Cela s'est produit à une échelle que peu de gens auraient pu imaginer, car les médias sociaux et autres réseaux en ligne ont englobé les interactions humaines dans des mesures facilement quantifiables, telles qu'être amis ou non, aimer ou non, un suiveur ou quelqu'un qui est suivi. Et les données générées par ces interactions ont été utilisées pour façonner davantage le comportement, en ciblant des messages destinés à manipuler psychologiquement les gens.

En 2001, il écrivait que « votre visage n'est pas un code-barres », s'opposant à l'utilisation de la reconnaissance faciale dans les lieux publics. Dans l'article, il a prédit que, si la technologie continuait à se développer en Occident, elle finirait par être adoptée ailleurs, permettant, par exemple, au gouvernement chinois de suivre tout le monde à l'intérieur de son pays d'ici 20 ans.

Vingt ans plus tard, un débat fait rage aux États-Unis sur l'utilisation de la technologie de reconnaissance faciale par les forces de l'ordre et les agents de l'immigration, et certains États ont commencé à interdire cette technologie dans les lieux publics. Malgré le tollé, il est peut-être trop tard pour freiner la prolifération de la technologie. La Chine, comme Agre l'avait prédit, a déjà commencé à l' employer à grande échelle, permettant un niveau de surveillance sans précédent de la part du Parti communiste.

Agre a fait connaître son travail dans le grand public avec une liste de diffusion Internet appelée Red Rock Eater News Service, du nom d'une blague dans le « Livre des énigmes » de Bennett Cerf. Il est considéré comme l'un des premiers exemples de ce qui deviendrait éventuellement des blogs.

Agre était aussi, parfois, profondément frustré par les limites de son travail, qui était si en avance sur son temps qu'il est resté lettre morte jusqu'à 25 ans plus tard. « Il avait l'impression que les gens ne comprenaient pas ce qu'il disait. Il écrivait pour un public d'obsédés et les obsédés étaient incapables de comprendre ce qu'il disait », a déclaré Bowker.

« Rien ne peut arrêter ce qui s'en vient » : les forums d'extrême droite qui ont fomenté les émeutes du Capitole s'en réjouissent

« Il était certainement frustré qu'il n'y ait pas eu plus d'adhésion. Mais les gens qui ont une génération d'avance sur eux-mêmes, ils ont toujours une génération d'avance sur eux-mêmes », a déclaré Borgman.

Le projet final d'Agre était ce que ses amis et collègues appelaient familièrement « La Bible d'Internet », un livre définitif qui disséquerait les fondements d'Internet à partir de zéro. Mais il ne l'a jamais terminé.

Agre refait surface de temps en temps, selon un ancien collègue, mais n'a pas été vu depuis des années.

« Pourquoi certains types d'érudits perspicaces ou même de personnes ayant une compréhension aussi perspicace d'un domaine lèvent-ils les bras en l'air et partent, j'en ai fini avec ça ? » a demandé Simon Penny, professeur de beaux-arts à l'Université de Californie à Irvine qui a beaucoup étudié le travail d'Agre. «Psychologiquement, les gens ont ces pauses. C'est une grande question. Qui continue et pourquoi ? Qui continue à être engagé dans une sorte de bataille, une sorte de projet intellectuel et jusqu'où vont-ils, j'en ai fini ? Ou dites : « Ceci n'est plus pertinent pour moi et j'ai vu l'erreur de mes voies. »

Il y a plusieurs années, d'anciens collègues de l'UCLA ont tenté de rassembler une collection de son travail, mais Agre a refait surface, leur disant d'arrêter.

Le travail de toute une vie d'Agre est resté inachevé, des questions posées mais sans réponse. John Seberger, un boursier postdoctoral au département d'informatique de l'Université de l'Indiana qui a beaucoup étudié les travaux d'Agre, a déclaré que ce n'était pas nécessairement une mauvaise chose.

Seberger a déclaré que le travail d'Agre offre une façon de réfléchir aux problèmes auxquels est confrontée une société de plus en plus numérique. Mais aujourd'hui, plus d'une décennie après la disparition d'Agre, les problèmes sont mieux compris et il y a plus de gens qui les étudient.

"Surtout en ce moment où nous sommes confrontés à de profonds troubles sociaux, la possibilité d'impliquer des groupes d'universitaires plus divers pour répondre à ces questions qu'il a laissées sans réponse ne peut que nous être bénéfique", a-t-il déclaré.

Par Reed Albergotti

Reed Albergotti est le journaliste électronique grand public du Washington Post, emmenant les lecteurs dans des entreprises puissantes et secrètes telles qu'Apple et mettant en lumière l'industrie trouble et mondiale responsable de la construction de la myriade d'appareils qui touchent tous les aspects de nos vies. Il a passé 12 ans au Wall Street Journal et quatre à l'Information.

TWP