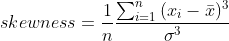Generative Pre-trained Transformer 3 (GPT-3) is an autoregressive language model that generates text using algorithms that are pre-trained. It was created by OpenAI (a research business co-founded by Elon Musk) and has been described as the most important and useful advance in AI for years.
Last summer writer, speaker, and musician, K Allado-McDowell initiated a conversation with GPT-3 which became the collection of poetry and prose Pharmako-AI. Taking this collection as her departure point, Warburg PhD student Beatrice Bottomley reflects on what GPT-3 means for how we think about writing and meaning.
GPT-3 is just over nine months old now. Since the release of its beta version by the California- based company Open AI in June 2020, the language model has been an object of fascination for both technophiles and, to a certain extent, laypersons. GPT-3 is an autoregressive language model trained on a large text corpus from the internet. It uses deep-learning to produce text in response to prompts. You can direct GPT-3 to perform a task by providing it with examples or through a simple instruction. If you open up the twitter account of Greg Brockman, the chairman of Open AI, you can find examples of GPT-3 being used to make computer programs that write copy, generate code, translate Navajo and compose libretti.
Most articles about GPT-3 will use words like “eerie” or “chilling” to describe the language model’s ability to produce text like a human. Some go further to endow GPT-3 with a more-than-human or god-like quality. During the first summer of the coronavirus pandemic, K Allado-McDowell initiated a conversation with GPT-3, which would become the collection of poetry and prose Pharmako-AI. Allado-McDowell found not only an interlocutor, but also co-writer in the language model. When writing of GPT-3, Allado-McDowell gives it divine attributes, comparing the language model to a language deity:
“The Greek god Hermes (counterpart to the Roman Mercury) was the god of translators and interpreters. A deity that rules communication is an incorporeal linguistic power. A modern conception of such might read: a force of language from outside of materiality. Automated writing systems like neural net language models relate to geometry, translation, abstract mathematics, interpretation and speech. It’s easy to imagine many applications of these technologies for trade, music, divination etc. So the correspondence is clear. Intuition suggests that we can think the relation between language models and language deities in a way that expands our understanding of both.”
What if we follow Allado-McDowell’s suggestion to consider the relationship between GPT-3 and the language deity Hermes? I must admit that I would hesitate before comparing GPT-3 to a deity. However, if I had to compare the language model to a god, they would be Greek; like Greek gods, GPT-3 is not immune to human-like vagary and bias. Researchers working with Open-AI found that GPT-3 retains the biases of the data that it has been trained on, which can lead it to generate prejudiced content. In that same paper, Brown et al. (2020) also noted that “large pre-trained language models are not grounded in other domains of experience, such as video or real-world physical interaction, and thus lack a large amount of context about the world.” Both the gods and GPT-3 could be considered, to a certain extent, dependent on the human world, but do not interact with it to the same degree as humans.

Lead votive images of Hermes from the reservoir of the aqueduct at ‘Ain al-Djoudj near Baalbek (Heliopolis), Lebanon, (100-400 CE), Warburg Iconographic Database.
Let us return to Hermes. As told by Kerenyi (1951) in The Gods of the Greeks, a baby Hermes, after rustling fifty cows, roasts them on a fire. The smell of the meat torments the little god, but he does not eat; as gods “to whom sacrifices are made, do not really consume the flesh of the victim”. Removed from sensual experience of a world that provides context for much human writing, GPT-3 can produce both surreal imagery and factual inaccuracies. In Pharmako-AI, GPT-3, whilst discussing the construction of a new science, which reflects on “the lessons that living things teach us about themselves”, underlines that “This isn’t a new idea, and I’m not the only one who thinks that way. Just a few weeks ago, a group of scientists at Oxford, including the legendary Nobel Prize winning chemist John Polanyi, published a paper that argued for a ‘Global Apollo Program’ that ‘would commit the world to launch a coordinated research effort to better understand the drivers of climate change…”. Non sequitur aside, a couple of Google searches reveal that the Global Apollo Programme was launched in 2015, not 2020, and, as far as I could find, John Polanyi was not involved.
Such inaccuracies do not only suggest that GPT-3 operates at a different degree of reality, but also relate to the question of how we produce and understand meaning in writing. From Aristotle’s De Interpretatione, the Greeks developed a tripartite theory of meaning, consisting of sounds, thoughts and things (phōnai, noēmata and pragmata). The Medieval Arabic tradition developed its own theory of meaning based on the relationship between vocal form (lafẓ) and mental content (maʿnā). Mental content acts as the intermediary between vocal form and things. In each act of language (whether spoken or written), the relationship between mental content and vocal form is expressed. Avicenna (d.1037) in Pointers and Reminders underlined that this relationship is dynamic. He claimed that vocal form indicated mental content through congruence, implication and concomitance and further suggested that the patterns of vocal form may affect the patterns of mental content. Naṣīr al-Dīn al-Ṭūsī (d.1274) brought together this idea with the Aristotelian tripartite division of existence to distinguish between existence in the mind, in entity, in writing and in speech.
When producing text, GPT-3 does not negotiate between linguistic form and mental content in the same way as humans. GPT-3 is an autoregressive language model, which offers predictions of future text based on its analysis of the corpus. Here the Hermes analogy unwinds. Unlike Hermes, who invented the lyre and “sandals such as no one else could devise” (Kerenyi, 1951), GPT-3 can only offer permutations based on a large, though inevitably limited and normative, corpus created by humans. Brown et al. (2020) note “its [GPT-3’s] decisions are not easily interpretable.” Perhaps this is unsurprising, as GPT-3 negotiates between patterns in linguistic form, rather than between the linguistic, mental and material. Indeed, GPT-3’s reality is centred on the existence of things in writing rather than in the mind or entity, and thus it blends, what might be referred to as, fact and fiction.

Hermes as messenger in an advert for Interflora,(1910-1935), Warburg Iconographic Database.
By seeking a co-writer in GPT-3, Allado-McDowell takes for granted that what the language model is doing is writing. However, taking into account an understanding of language and meaning as developed by both the Greek and Islamic traditions, one might ask – does GPT-3 write or produce text? What is the difference? Is what GPT-3 does an act of language?
To a certain extent, these questions are irrelevant. GPT-3 remains just a (complex) tool for creating text that is anchored in human datasets and instruction. It has not yet ushered in the paradigm shift whispered of by reviewers and examples of its use are often more novel than practical (though perhaps this isn’t a bad thing for many workers). However, were GPT-3, or similar language models, to become more present in our lives, I would want to have a clearer grasp of what it meant for writing. As Yuk Hui (2020) points out in his article Writing and Cosmotechnics, “to write is not simply to deliver communicative meaning but also to ponder about the relation between the human and the cosmos.” In acknowledging GPT-3 as an author, would we not only need to make room for different theories of meaning, but also different ways of thinking about how humans relate to the universe?
Beatrice Bottomley is a doctoral student at the Warburg Institute, University of London, supported by a studentship from the London Arts and Humanities Partnership (LAHP). Her research examines the relationship between language and existence in Ibn ʿArabi’s al-Futūḥāt al-Makkiyya, “The Meccan Openings”. Beatrice’s wider research interests include philosophies of language, translation studies and histories of technology. Beatrice also works as a translator from Arabic and French to English.
Beatrice was introduced to the work of K Allado-McDowell after hearing them speak last December in an event that celebrated the launch of two new books, Aby Warburg: Bilderatlas Mnemosyne: The Original and The Atlas of Anomalous AI. Watch the event recording here.