John von Neumann’s Minimax Theorem

“As far as I can see, there could be no theory of games … without that theorem … I thought there was nothing worth publishing until the Minimax Theorem was proved” — John von Neumann
Hungarian polymath John von Neumann (1903–1957)’s legacy includes significant contributions to the foundations of mathematics and set theory, quantum mechanics and ergodic theory, in addition to early work on computers, nuclear energy and artificial intelligence. Indeed, von Neumann’s output was so considerable in the period from 1925 to the 1950s that to this day, his co-invention of game theory is still often mentioned as a sidenote.
Make no mistake: Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games, with a proof provided by John von Neumann in 1928, included in the paper auspiciously titled:
- von Neumann, J. (1928). Zur Theorie der Gesellschaftsspiele (“The Theory of Games”). Mathematische Annalen 100, pp. 295–320.
Sixteen years later, his paper was followed by the 1944 book Theory of Games and Economic Behaviour*, co-written with Oskar Morgenstern (1902–77), considered the first significant book on game theory. In addition to two-person cooperative games, the book also includes analyses of games with multiple players. Considered a classic, the first edition has later been followed up by second (1947), third (1953), fourth (1974) and 60th anniversary editions (2007).
The purpose of this essay is to explain the context of von Neumann’s momentous 1928 minimax theorem to a general audience. In explaining von Neumann’s theorem, the essay makes extensive use of two wonderful books:
- Leonard, R. J. (2010). ‘Von Neumann, Morgenstern, and the Creation of Game Theory: From Chess to Social Science*’, 1900–1960. Cambridge University Press.
- Dimand, M.A., & Dimand, R.W. (1996). ‘The History of Game Theory, Volume I: From the beginnings to 1945’. Routledge Research.
Estimated reading time is 10 minutes.
The Theory of Games
The history of game theory can be traced back as far as to 1713, when Earl James Waldegrave (1864–1741) analyzed and provided a minimax mixed strategy solution to the card game “Le Her”:
The "Le Her" Game
To play, the dealer gives one card to the receiver and one to the dealer. The receiver may choose to exchange cards with the dealer, unless the dealer has a king, in which case no exchange occurs. Then, the dealer may choose to exchange with the top card of the deck, unless the top card is a king, in which case no exchange occurs. In the case of the dealer and receiver having same ranked cards, the dealer is the winner.The game is described as follows in the 1865 book ‘A History of the Mathematical Theory of Probability from the Time of Pascal to that of Laplace’ by Isaac Todhunter (Dimand & Dimand, 1996 p. 121):
Peter holds a common pack of cards; he gives a card at random to Paul and takes one himself; the main object is for each to obtain a higher card than his adversary.The order of value is ace, two, three, ..., ten, Knight, Queen, King. Now, if Paul is not content with his card he may compel Peter to change with him. However, if Peter has a King he is allowed to retain it.If Peter is not content with the card which he at first obtained, or which he has been compelled to receive from Paul, he is allowed to change it for another taken out of the deck at random. However, if the card Peter then draws is a King he is not allowed to have it, and must retain the card with which he was dissatisfied. If Paul and Peter finally have cards of the same value, Paul is considered to lose.- Excerpt, 'A History of the Mathematical Theory of Probability from the Time of Pascal to that of Laplace' by Todhunter (1865 p. 106)
Waldegrave’ mixed strategy solution concluded that (Dimand & Dimand, 1996):
- Peter should hold cards eight and above, and exchange lower cards with probability = 62.5%
- Peter should exchange cards eight and below, and hold higher cards with probability = 37.5%
- Paul should hold seven and above with probability = 37.5%
His solution survives in a 1713 letter written by Pierre Remond de Montmort (1678–1719) to Johann Bernoulli (1667–1748), who disagreed slightly with Waldegrave’s solution, arguing that that both players should change cards in doubtful cases. Apart from de Montmort’s publication of his correspondence with Bernoulli, Waldegrave’s solution remained unpublished until Isaac Todhunter (1820–1884)’s inclusion of the strategy in his 1865 book (Dimand & Dimand, 1996).
Other examples of early game theoretic analyses include James Madison (1751–1836)’s analysis of the ways states can be expected to behave under different systems of taxation and Antoine August Cournot (1801–1877)’s 1838 analysis of Nash equilibrium solutions in duopoly. In 1913 Ernst Zermelo (1871–1953) proved that the optimal strategy is chess is strictly determined, i.e. that the game has at least one Nash equilibrium where both players use pure strategies. All of these early examples of course preceded John F. Nash’s 1949 invention of non-cooperative game theory.
John von Neumann’s 1928 Paper

Hungarian polymath John von Neumann (1903–1957) first turned his attention to game theory in 1926, while still an apprentice of David Hilbert (1862–1943) at the University of Göttingen. von Neumann had been working on the axiomatization of set theory since 1923 and just begun his work on establishing a rigorous mathematical framework for quantum mechanics. According to Leonard (1992):
“At some point in 1926, von Neumann produced his proof of the minimax theorem, which, not surprisingly, was overshadowed by his contemporaneous work.”
The source of his interest in games thus remains something of a mystery. His methodology, however, by way of an axiomatic approach is clearly derived from his work in Hilbertian set theory. Indeed too, as Leonard (1992) notes, is “the notion of chance, made central through probabilistiuc play” which is “consonant with the indeterminism at the basis of quantum mechanics”. As von Neumann notes in his 1928 paper,
“Chance […] is such an intrinsic part of the game itself (if not the world) that there is no need to introduce it artificially by way of the rules of the game […] it will assert itself” — von Neumann (1928)
MiniMax & MaxiMin
Historically, there were thought to be two approaches to optimizing the outcome of games such as Le Her:
- The conservatively greedy approach (called maximin)
- The conservatively aggressive approach (called minimax)
The MaxiMin Approach
An agent A whose choices are governed by a maximin criterion looks at each strategy she might follow and, in each case, considers the lowest payoff she can receive by following such strategies.She then chooses to play the strategy whose minimum payoff is the highest.
As the authors note, agent A’s strategy her is extremely conservative and pessimistic. This because, the strategy places much if not most of its emphasis on agent B’s ability to deliver A her lowest payoff possible. Player A ensures her minimal payoff by taking this approach.
The MiniMax Approach
Another player, C, taking the minimax approach on the other hand, looks at the payoffs her opponent D can achieve given each strategy of C. C then chooses to play the strategy which will give D the lowest payoff, if D would always plays so to maximize his payoff subject to C's strategy.As Dimand & Dimand (1996) write, ‘while the maximum approach presumes a player who wishes to guarantee her own minimum payoff, minimax conjectures a player who wants to guarantee her opponent’s maximum’s payoff. While the maximin player is conservatively greedy, the minimax player is conservatively aggressive’.
von Neumann’s Minimax Theorem (1928)


Any event may be regarded as a game of strategy if one looks at the effect it has on the participants, given the external conditions and provided the participants are acting of their own free will.- Excerpt, Zur Theorie der Gesellschaftspiele by von Neumann (1928)
At some point in 1926, it is not known when, von Neumann produced his proof of the minimax theorem. von Neumann presented his first result to the Göttingen Mathematical Society, on December 7th 1926, three weeks before his 23rd birthday. His proof was complicated, as it combined both elementary and topological concepts in “a manner not easy for the reader to follow, but it was a valid proof nonetheless” (Dimand & Dimand, 1996). The result was published in two articles in 1928, the proof only the latter:
- von Neumann, J. (1928a). Sur la théorie des jeux (“On Game Theory”). Comptes Rendus de l’Académie des Sciences, 186 (25): 1689–91.
- von Neumann, J. (1928b). Zur Theorie der Gesellschaftsspiele (“The Theory of Games”). Mathematische Annalen 100: 295–320.
French mathematician Émile Borel (1871–1956) had published four notes on strategic games between 1921–27, around the same time von Neumann was developing the result for his 1928 paper. von Neumann states in a communication to Borel that his proof had been achieved in 1926. He makes sure to remark that he reached this result independently (Leonard, 1992):
“M’étant occupé indépendamment avec le même problème”
As he writes in a footnote:
“While this paper was put into its final form, I learned of the note of E. Borel in the Comptes Rendus of Jan. 10, 1927. Borel formulates the question of bilinear forms for a symmetric two-person game and states that no examples for MaxMin < MinMax are known. Our results above answer his questions”
von Neumann (1928a) is one of his letters (in French) to Borel, which Borel later presented to l’Académie des Sciences. In the communication, von Neumann footnotes that his proof has been accepted for publication and will be forthcoming in Mathematische Annalen 100 under the title Zur Theorie der Gesellschaftsspiele. Reportedly, von Neumann had sent his manuscript to Mathematische Annalen as early as in July 1927. The publication (von Neumann, 1928b) came a few months after his communication to Borel (von Neumann, 1928a). Written in German, the paper contains von Neumann’s long and difficult proof of the existence of an equilibrium value for the two-person, discrete game. A translation of his paper appears in Tucker and Luce’s Contributions to the Theory of Games, Volume IV.
A minimax theorem (such as von Neumann’s 1928 result) provides the conditions that guarantee that the max-min inequality is also an equality, i.e. that
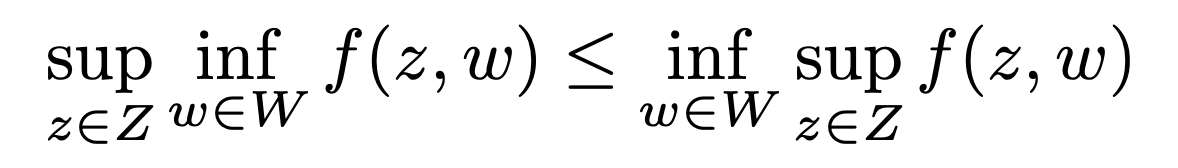
von Neumann’s minimax theorem in other word shows that two-person zero-sum games with finitely many pure strategies (or a continuum of pure strategies and continuous convex payoffs) have solutions (equilibria) under maximin and minimax strategies which are identical (Dimand & Dimand, 1996). Such a solution guarentees a player that they are minimizing the possible loss in a worst case scenario.
Later Work
In 1937 — utilizing L. E. J. Brouwer (1881–1966)’s fixed-point theorem on continuous mappings into compact convex sets — von Neumann provided a purely topological proof of the existence of general competitive equilibrium, a much clearer and more elegant proof than that included in his 1928 paper:
- von Neumann, J. (1937). ‘Über ein Oikonomisches Gleichungssystem und eine Verallgemeinerung des Brouwerschen Fixpunktsatzes’ in in Menger, K. (ed). Ergebnisse eines Mathematischen Seminars. Vienna.
Weintraub (2002) later referred to the paper as ‘the most important paper in mathematical economics’, as it was the genesis of both 1) modern existence proofs in general equilibrium models, 2) linear programming and dual systems of inequalities, 3) turnpike theory and 4) fixed-point theory.
The first purely elementary proof of the minimax theorem came a year after von Neumann’s 1937 paper, when Borel’s student Jean Ville (1910–89) utilized convexity arguments and the concept of a supporting hyperplane to show the same result, included in one of Borel’s books:
- Ville, J. (1938). ‘Sur le théorié générale des jeux où intervient l’habiliité des joueurs’. In Borél et al (ed.), vol. 4. Applications des jeux de hasard, p. 105–13.
In the same chapter, Ville also gave the first proof of the minimax theorem for the case of a continuum of possible pure strategies (Dimand & Dimand, 1996).
Theory of Games and Economic Behavior
Aside from von Neumann’s 1928 and 1937 papers, the brief notes of Borel and the proof of Ville (1938), relatively little formal work on the definition and existence of equilibrium for games was published before von Neumann and Morgenstern’s monumental 1944 book Theory of Games and Economic Behavior (Dimand & Dimand, 1996). The two first met in Princeton in 1938, but didn’t begin discussing theories of games until 1939, before collaborating intensely in the period 1941–44 to develop what became the first extensive book on game theory:
- von Neumann, J. & Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton University Press.
WRITTEN BY
Editor at Cantor’s Paradise. Assistant Professor at the Norwegian University of Science and Technology.



